
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LD
3

Các câu hỏi dưới đây có thể giống với câu hỏi trên
LA
1
PH
0


BT
14 tháng 3 2017
M=(6n+4-5):(3n+2)=2-5:(3n+2)
a) để M nguyên thì (3n+2) phải là ước của 5
=> 3n+2={-5; -1; 1; 5}
+/ 3n+2=-5 => n=-7/3 (loại)
+/ 3n+2=-1 => n=-1; M=7
+/ 3n+2=1 => n=-1/3 loại
+/ 3n+2=5 => n=1; M=-3
Đs: n={-1; 1}
b) để M đạt nhỏ nhất thì 5:(3n+2) là lớn nhất, hay 3n+2 đạt giá trị nhỏ nhất => n=0
Mmin=2-5/2=-1/2
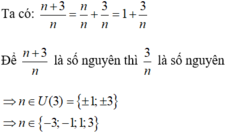
ĐKXĐ: \(n\ne\dfrac{1}{3}\)
Để \(\dfrac{n+7}{3n-1}\in Z\) thì \(n+7⋮3n-1\)
=>\(3n+21⋮3n-1\)
=>\(3n-1+22⋮3n-1\)
=>\(3n-1\inƯ\left(22\right)\)
=>\(3n-1\in\left\{1;-1;2;-2;11;-11;22;-22\right\}\)
=>\(3n\in\left\{2;0;3;-1;12;-10;23;-21\right\}\)
=>\(n\in\left\{\dfrac{2}{3};0;1;-\dfrac{1}{3};4;-\dfrac{10}{3};\dfrac{23}{3};-7\right\}\)
mà n là số tự nhiên
nên \(n\in\left\{0;1;4\right\}\)
Ta có: \(\dfrac{n+7}{3n-1}\in Z\Rightarrow\dfrac{3\left(n+7\right)}{3n-1}\in Z\)
\(\dfrac{3\left(n+7\right)}{3n-1}=\dfrac{3n+21}{3n-1}=\dfrac{3n-1+22}{3n-1}=1+\dfrac{22}{3n-1}\)
⇒ 22 ⋮ 3n + 1
⇒ 3n - 1 ∈ Ư(22)={1; -1; 2; -2; 11; -11; 22; -22}
⇒ 3n ∈ {2; 0; 3; -1; 12; -10; 23; -21}
⇒ n ∈ \(\left\{\dfrac{2}{3};0;1;-\dfrac{1}{3};4;-\dfrac{10}{3};\dfrac{23}{3};-7\right\}\)
Mà: n ∈ N
\(\Rightarrow n\in\left\{0;1;4;7\right\}\)