
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo mình thì phân tích ra thành thế này
gọi số cần tìm là \(ab\) có:
\(ab=x^3;a+b=x^2\)(\(x\) là số tự nhiên mà khi lập phương lên thì bằng \(ab\), khi bình phương lên thì bằng \(a+b\))
Từ đó ta có: \(10a+b=x^3\)
\(a+b=x^2\)
Rồi suy ra được ab thì phải, mình không biết có đúng không nữa, nếu mà các bước mình làm đúng thì bạn nghiên cứu thêm nhé

https://olm.vn/hoi-dap/question/116557.html
Bn tìm theo đường link này nhé, cô Loan đã giải thích rõ r` đó!

Gọi ba chữ số của số phải tìm là a, b, c
![]()
Số phải tìm là bội của 18 nên số đó chia hết cho 9 , do đó a + b + c= 9 hoặc a + b + c = 18 hoặc a + b + c =27
Theo đề bài, các chữ số của số đó tỉ lệ với 1;2;3 nên
a 1 = b 2 = c 3
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
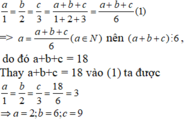
Lại có số phải tìm là bội của 18 nên chữ số hàng đơn vị của nó là số chẵn, do đó có hai số thỏa mãn đề bài là 396;936
Đáp án cần chọn là C

gọi 3 chữ số của số cần tìm là a,b,c ( a,b,c \(\in\)N ; a\(\ne\)0, a,b,c, \(\le\)9 )
Theo đầu bài ta có :
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\)\(\Rightarrow\frac{a}{1}=\frac{a+b+c}{1+2+3}\)\(\Rightarrow a=\frac{a+b+c}{6}\)
Do vậy : a + b + c \(⋮\)6 ( 1 )
Mặt khác số đó chia hết cho 18 nên số đó chia hết cho 9 \(\Rightarrow\)a + b + c \(⋮\)9 ( 2 )
Mà 0 < a + b + c \(\le\)27 ( 3 )
Từ ( 1 ), ( 2 ) và ( 3 ) \(\Rightarrow\)a + b + c \(⋮\)18
Ta có : \(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=3\)\(\Rightarrow a=3,b=6,c=9\)
\(\Rightarrow\)số đó là 396 hoặc 936


gọi chữ số nhỏ nhất phải tìm là a => số có 3 chữ số phải tìm là a;2a;3a với 3a \(\le\)9=> a\(\le\)3. Do số phải tìm chia hết cho 18 tức chia hết cho 9 nên \(\left(a+2a+3a\right)=6a\)chia hết cho 9 => a chia hết cho 3 vậy a=3 => 3 chữ số là 3;6;9
Số cần tìm là số chẵn nên chữ số cuối là 6
=> số cần tìm là 396 hoặc 936