Tìm số nguyên x, sao cho 4x + 1 chia hết cho 2x

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

26 tháng 7 2017

Tìm số nguyên x, sao cho 4x + 1 chia hết cho 2x – 3

#Toán lớp 6

Cao Minh Tâm

26 tháng 7 2017

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Hoàng Vi Ánh

3 tháng 4 2020 - olm

Tìm các số nguyên x sao chi :
4x + 1 chia hết cho 2x - 3
2x - 3 chia hết cho 4x + 1

#Toán lớp 6

Ngọc Lan

3 tháng 4 2020

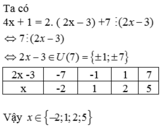
Ta có : 4x+1 chia hết cho 2x-3

=> 4x-6+7 chia hết cho 2x-3

=> 2(2x-3)+7 chia hết cho 2x-3

=> 7 chia hết cho 2x-3

=> 2x-3 thuộc Ư(7)={-7;-1;1;7}

... (bạn tự làm nhé!)

Ta có : 2x-3 chia hết cho 4x+1

=> 4x-6 chia hết cho 4x+1

=> 4x+1-7 chia hết cho 4x+1

=> 7 chia hết cho 4x+1

...

Học tốt!

Đúng(0)

Pham Trong Bach

11 tháng 2 2019

Tìm số nguyên x sao cho 4x + 1 chia hết cho 2x - 3

#Toán lớp 6

Cao Minh Tâm

11 tháng 2 2019

Đúng(0)

tran thu thuy

7 tháng 1 2016 - olm

Tìm số nguyên x sao cho:

a) 4x + 3 chia hết cho x - 2

b)2x + 7 chia het cho x+ 3

#Toán lớp 6

hoang nguyen truong giang

7 tháng 1 2016

b) 2x + 7 chia hết cho x + 3

=> 2x + 6 + 1 chia hết cho x + 3

=> 2(x + 3) + 1 chia hết cho x + 3

Mà 2(x + 3) chia hết cho x + 3

=> 1 chia hết cho x + 3

=> x + 3 \(\in\){-1;1}

=> x \(\in\){-4;-2}

Đúng(0)

Lê Chí Cường

7 tháng 1 2016

a)4x+3 chia hết cho x-2

4x-8+11 chia hết cho x-2

4(x-2)+11 chia hết cho x-2

=>11 chia hết cho x-2 hay x-2EƯ(11)={1;-1;11;-11}

=>xE{3;1;13;-9}

b)2x+7 chia hết cho x+3

2x+6+1 chia hết cho x+3

2(x+3)+1 chia hết cho x+3

=>1 chia hết cho x+3 hay x+3EƯ(1)={1;-1}

=>xE{-2;-4}

Đúng(0)

Lưu Bảo Ngọc

17 tháng 12 2021

Bài 1.Tìm số nguyên n sao cho n+6 chia hết cho n+2

Bài 2. Tìm số nguyên n sao cho 3n+2 chia hết cho n+1

Bài 3. Tìm số nguyên x biết (x-2).(x+3)<0

Bài 4. Tìm số nguyên x biết (4-2x).(x+3)>0

#Toán lớp 6

Nguyễn Lê Phước Thịnh

17 tháng 12 2021

Bài 3:

=>-3<x<2

Đúng(3)

Nguyen Ha Thai 12

18 tháng 2 2020 - olm

Tìm số nguyên x saocho 4x +1 chia hết cho 2x-3

#Toán lớp 6

Trí Tiên

18 tháng 2 2020

\(4x+1⋮2x-3\)

\(\Leftrightarrow2\left(2x-3\right)+7⋮2x-3\)

\(\Leftrightarrow7⋮2x-3\)

\(\Leftrightarrow2x-3\inƯ\left(7\right)\)

\(\Leftrightarrow2x-3\in\left\{1,-1,7,-7\right\}\)

\(\Leftrightarrow x\in\left\{2,1,5,-2\right\}\)

Đúng(0)

Nguyễn Hoàng Diệu Linh

18 tháng 2 2020

bạn Đạt làm đúng rồi đấy!!!

Đúng(0)

Thùy Linh V Sone

3 tháng 3 2015 - olm

1/ Tìm tập hợp các số nguyên x sao cho 6 chia hết cho x-1

2/ Tìm tập hợp các số nguyên x sao cho 14 chia hết cho 2x+3

#Toán lớp 6

SNSD in my heart

4 tháng 3 2015

Mk nghĩ là như thê này

Câu 1:

6 chia hết cho x-1 => x-1 là ước của 6.Mà Ư(6)={1;-1;2;-2;3;-3;6;-6}=> x={2;0;3;-1;4;-2;7;-5}

Câu 2;

14 chia hết cho 2x+3

=>2x+3 là ước của 14.Mà Ư(14)={1;-1;2;-2;7;-7;14;-14}

=>x={-1;-2;2;-5;}

Đúng(0)

baby kute

3 tháng 3 2015

a, vì 6 chia hết cho x-1 suy ra x-1 thuộc ước của 6

vậy thuộc tập các phần tử là : 0;2;-1;3;-2;4;-5;7

vì 14 chia hết cho 2x+3 nên 2x+3 thuộc ước của 14

vì 2x+3 lẻ nên x+3 thuộc tập các phần tử là 1;-1;7;-7

vậy x thuộc tập các phần tử là -2;-1;-5;2

Đúng(0)

Lê Thị Khánh Linh

23 tháng 11 2021 - olm

tìm số tự nhiên x sao cho 4x + 3 chia hết cho 2x-1

#Toán lớp 6

Dương Nguyễn

15 tháng 10 2015 - olm

tìm số tự nhiên x sao cho 4x+3 chia hết cho 2x-1

#Toán lớp 6

Minh Hiền

15 tháng 10 2015

4x+3 chia hết cho 2x-1

=> 4x-2+5 chia hết cho 2x-1

=> 2(2x-1)+5 chia hết cho 2x-1

mà 2(2x-1) chia hết cho 2x-1

=> 5 chia hết cho 2x-1

=> \(2x-1\inƯ\left(5\right)=\left\{1;5\right\}\)

=>\(2x\in\left\{2;6\right\}\)

=>\(x\in\left\{1;3\right\}\)

Đúng(0)

Erza Scalet

22 tháng 1 2017

TỚ THẤY BẠN NÊN GIẢI THÍCH TẠI SAO LẠI NHƯ VẬY ĐỂ BẠN ẤY HIỂU BÀI VÀ LÀM ĐƯỢC BÀI KHÁC CHỨ( GỬI MINH HIỀN)

Đúng(0)

tố vân lê

19 tháng 1 2018 - olm

giải các bài toán sau :

a) tìm số nguyên n sao cho n+2 chia hết cho n-3

b) tìm các giá trị nguyên của x để x-3 là ước của 13

c) tìm các giá trị nguyên của x để x-2 là ước của 111

d) tìm các số nguyên n sao cho 5 chia hết cho n+ 15

e) tìm các số nguyên n sao cho 3 chia hết cho n+ 24

f) tìm các số nguyên sao cho : ( 4x + 3 ) chia hết ( x-2 )

giúp mình với !!!

#Toán lớp 6

Ánh Nguyễn

3 tháng 5 2021

a)n=5

b)X=16;-10;2;4

c)x=113;39;5;3;1;-1;-35;-109

Đúng(0)

Yen Nhi

23 tháng 11 2021

Answer:

a) \(\left(n+2\right)⋮\left(n-3\right)\)

\(\Rightarrow\left(n-3+5\right)⋮\left(n-3\right)\)

\(\Rightarrow5⋮\left(n-3\right)\)

\(\Rightarrow n-3\) là ước của \(5\), ta có:

Trường hợp 1: \(n-3=-1\Rightarrow n=2\)

Trường hợp 2: \(n-3=1\Rightarrow n=4\)

Trường hợp 3: \(n-3=5\Rightarrow n=8\)

Trường hợp 4: \(n-3=-5\Rightarrow n=-2\)

b) Ta có: \(x-3\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)

\(\Rightarrow x\in\left\{4;16;2;-10\right\}\)

Vậy để \(x-3\inƯ\left(13\right)\Rightarrow x\in\left\{4;16;2;-10\right\}\)

c) Ta có: \(x-2\inƯ\left(111\right)\)

\(\Rightarrow x-2\in\left\{\pm111;\pm37;\pm3;\pm1\right\}\)

\(\Rightarrow x\in\left\{-99;-35;1;1;3;5;39;113\right\}\)

d) \(5⋮n+15\Rightarrow n+15\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)

Trường hợp 1: \(n+15=-1\Rightarrow n=-16\)

Trường hợp 2: \(n+15=1\Rightarrow n=-14\)

Trường hợp 3: \(n+15=5\Rightarrow n=-10\)

Trường hợp 4: \(n+15=-5\Rightarrow n=-20\)

Vậy \(n\in\left\{-14;-16;-10;-20\right\}\)

e) \(3⋮n+24\)

\(\Rightarrow n+24\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)

\(\Rightarrow n\in\left\{-23;-25;-21;-27\right\}\)

f) Ta có: \(x-2⋮x-2\)

\(\Rightarrow4\left(x-2\right)⋮x-2\)

\(\Rightarrow4x-8⋮x-2\)

\(\Rightarrow\left(4x+3\right)-\left(4x-8\right)⋮x-2\)

\(\Rightarrow11⋮x-2\)

\(\Rightarrow x-2\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)

\(\Rightarrow x\in\left\{3;13;1;-9\right\}\)

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP