Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cần tìm là \(\overline{xy}\)
+) Do hiệu của 3 lần chữ số hàng chục với 2 lần chữ số hàng đơn vị là 11 nên ta có phương trình \(3x-2y=11\left(1\right)\)
+) Lại có, nếu đổi chữ số hàng chục và hàng đơn vị cho nhau, ta sẽ được 1 số mới nhỏ hơn số cũ 18 đơn vị, hay
\(\overline{xy}-\overline{yx}=18\Leftrightarrow\left(10x+y\right)-\left(10y+x\right)=18\Leftrightarrow9x-9y=18\Leftrightarrow x-y=2\left(2\right)\)
Từ (1) và (2), ta có hệ phương trình:
\(\left\{{}\begin{matrix}3x-2y=11\\x-y=2\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}3x-2y=11\\2x-2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=7\\y=5\end{matrix}\right.\)
Vậy số cần tìm là 75
Gọi số cần tìm là \(\overline{ab}\) (0<a<10; 0<b<10) => 3a - 2b = 11 (1)
Khi đổi chỗ hai chữ số cho nhau được số mới là \(\overline{ba}\)
Do số mới nhỏ hơn số cũ 18 đơn vị => \(\overline{ab}\) - \(\overline{ba}\) = 18
⇔ 10a + b - 10b - a = 18
⇔ 9a - 9b = 18 (2)
Từ (1) và (2) ta có hệ phương trình:\(\left\{{}\begin{matrix}3a-2b=11\\9a-9b=18\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}9a-6b=33\\9a-9b=18\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}-3b=-15\\9a-9b=18\end{matrix}\right.\)
⇔\(\left\{{}\begin{matrix}a=7\\b=5\end{matrix}\right.\) (tm)
Vậy số cần tìm là 75

Gọi a và b là số ban đầu ab
Tổng chữ số hàng chục và hai lần chữ số hàng đơn vị của 1 số có hai chữ số là 18
a + 2b = 18 (1)
Nếu đổi chỗ hai chữ số cho nhau thì được một số lớn hơn số ban đầu là 54 ba
(10b + a ) - ( 10a + b ) = 54 \(\Leftrightarrow\) -9a + 9b = 54 (2)
Từ (1) (2) ta suy ra hệ pt sau
\(\hept{\begin{cases}a+2b=18\\-9a+9b=54\end{cases}\Leftrightarrow\hept{\begin{cases}a=2\\b=8\end{cases}}}\)
Vậy số ban đầu là 28
CHÚC BỌN HỌC TỐT !! :))

Gọi x là chữ số hàng chục, y là chữ số hàng đơn vị.
Điều kiện: x, y ∈N*, 0 < x ≤ 9; 0 < y ≤ 9
Vì hai lần chữ số hàng chục lớn hơn 5 lần chữ số hàng đơn vị là 1 nên ta có: 2x – 5y = 1
Vì chữ số hàng chục chia cho chữ số hàng đơn vị được thương là 2 và dư cũng là 2 nên ta có: x = 2y + 2
Ta có hệ phương trình:
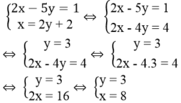
Giá trị của x và y thỏa mãn điều kiện bài toán.
Vậy số cần tìm là 83.

Lời giải:
Gọi số cần tìm là $\overline{ab}$. Điều kiện:.......
Theo bài ra ta có:
$a+2b=12(1)$
$\overline{a0b}-\overline{ab}=180$
$\Leftrightarrow 100a+b-(10a+b)=180$
$\Leftrightarrow 90a=180$
$\Leftrightarrow a=2(2)$
Từ $(1); (2)\Rightarrow b=5$
Vậy số cần tìm là $25$

Gọi số cần tìm là ab (a,b là chữ số ;a khác 0)
Theo đề bài a - b = 2 => a = b + 2
và ab - a2 - b2 = 1
=> 10a + b - (b + 2)2 - b2 = 1
=> 10b + 20 + b - b2 + 4b + 4 - b2 = 1
=> 15b + 24 - 2b2 = 1
=> b.(15 - 2b) = -23
=> b \(\in\) Ư(-23) = {-23; -1; 1; 23}
- Nếu b = -23 thì 15 - 2b = 61 (loại)
- Nếu b = -1 thì 15 - 2b = 17 (loại)
- Nếu b = 1 thì 15 - 2b = 13 (loại)
- Nếu b = 23 thì 15 - 2b = -31 (loại)
Vậy không tìm được số thỏa mãn đề bài
Gọi chữ số hàng đơn vị là a thì chữ số hàng chục là a + 2
Ta có số (a+2)a
Theo bài cho ta có:
=> (a+2)a = a2 + (a+2)2 + 1
=> 10(a+2) + a = a2 + a2 + 4a + 5
=> 11a + 20 = 2a2 + 4a + 5
=> 2a2 -7a+ 5 = 0
=> 2a2 - 2a - 5a + 5 = 0
=> 2a(a - 1) - 5(a - 1) = 0
=> (2a - 5)(a - 1) = 0
=> a - 1 = 0 hoặc 2a - 5 = 0
=> a = 1 (thỏa mãn) hoặc a = 5/2 (Loại)
Vậy số cần tìm là 31
