Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
Phương pháp
Nhẩm nghiệm của phương trình hoành độ giao điểm, từ đó tìm điều kiện để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.

Để đồ thị hàm số cắt trục hoành tại ba điểm phân biệt thì phương trình x 2 + ( m + 3 ) x + m 2 = 0 phải có hai nghiệm phân biệt khác 1
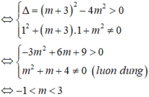
Do đó với -1<m<3 thì đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt
![]()

Đáp án C
YCBT ⇔ x 3 + 3 m x + m − 1 = 0 có một nghiệm
x = 2 ⇔ 8 + 6 m + m − 1 = 0 ⇔ m = − 1

Đáp án B.
Phương pháp: Tìm điều kiện để phương trình hoành độ giao điểm có ba nghiệm phân biệt thỏa mãn x A = 2 , hoặc x B < - 1 < x C < 1 hoặc - 1 < x B < 1 < x C
Cách giải:
Đồ thị hàm số y = x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 luôn đi qua điểm A(2;0)
Xét phương trình hoành độ giao điểm
x 3 - 2 ( m + 1 ) x 2 + ( 5 m + 1 ) x - 2 m - 2 = 0
![]()
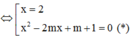
Để phương trình có 3 nghiệm phân biệt ó pt (*) có 2 nghiệm phân biệt khác 2
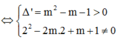
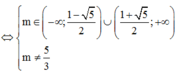
Giả sử x B ; x C ( x B < x C ) là 2 nghiệm phân biệt của phương trình (*).
Để hai điểm B, C một điểm nằm trong một điểm nằm ngoài đường tròn x2 + y2 = 1
TH1: ![]()
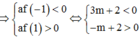
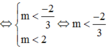
TH2: ![]()
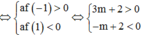
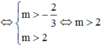
Kết hợp điều kiện ta có: 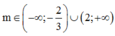
Lại có m ∈ [–10;100]
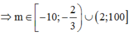
=> Có 108 giá trị m nguyên thỏa mãn yêu cầu bái toán






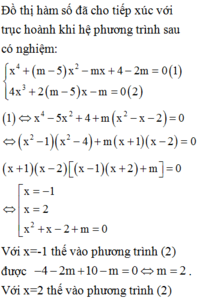

Ta có a = -1 < 0 và y ' = 0 ⇔ x = 0 x 2 = m + 2 nên dựa vào hình dáng của đồ thị hàm số ta xét các trường hợp sau để đáp ứng yêu cầu bài toán.
Hàm số chỉ có một cực trị âm ⇔ m + 2 ≤ 0 y 0 < 0 ⇔ - 4 < m ≤ - 2
Hàm số có ba cực trị và giá trị cực đại âm
⇔ m + 2 > 0 y ± m + 2 < 0 ⇔ - 2 < m < 0
Qua hai trường hợp trên ta thu được -4 < m < 0.
Do m ∈ Z nên m ∈ - 3 ; - 2 ; - 1 .
Vậy có 3 giá trị nguyên của m thỏa mãn yêu cầu bài toán
Đáp án C