Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có vectơ pháp tuyến của hai đường thẳng \({d_1}\)và \({d_2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( {1; - 2} \right),\overrightarrow {{n_2}} = \left( {3; - 1} \right)\)
Ta có \(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {1.3 + \left( { - 2} \right).( - 1)} \right|}}{{\sqrt {{1^2} + {{\left( { - 2} \right)}^2}} \sqrt {{3^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{\sqrt 2 }}{2} \Rightarrow \left( {{d_1},{d_2}} \right) = 45^\circ \)
b) Ta có vectơ pháp tuyến của hai đường thẳng \({d_1}\) và \({d_2}\) lần lượt là \(\overrightarrow {{n_1}} = \left( {5; - 1} \right),\overrightarrow {{n_2}} = \left( {1;5} \right)\)
Ta có \({a_1}{a_2} + {b_1}{b_2} = 5.1 + ( - 1).5 = 0\)
Suy ra \(\left( {{d_1},{d_2}} \right) = 90^\circ \)
c) Ta có vectơ chỉ phương của hai đường thẳng \({\Delta _1}\) và \({\Delta _2}\) lần lượt là \(\overrightarrow {{u_1}} = \left( {2; 4} \right),\overrightarrow {{u_2}} = \left( {1;2} \right)\)
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {2.1+4.2} \right|}}{{\sqrt {{2^2} + {{ { 4} }^2}} \sqrt {{1^2} + {{{ 2}}^2}} }} = 1 \Rightarrow \left( {{d_1},{d_2}} \right) = 0^\circ \)

Vecto pháp tuyến của đường thẳng \({d_1}\) là: \(\overrightarrow {{n_1}} = \left( {2; - 1} \right)\)
Vecto pháp tuyến của đường thẳng \({d_2}\) là: \(\overrightarrow {{n_2}} = \left( {1; - 3} \right)\)
Ta có: \(\cos \left( {{d_1},{d_2}} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ;\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {2.1 + \left( { - 1} \right).\left( { - 3} \right)} \right|}}{{\sqrt {{{\left( 2 \right)}^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{\sqrt 2 }}{2}\)
Vậy \(\left( {{d_1},{d_2}} \right) = {45^o}\)

a) Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ sau:
\(\left\{ \begin{array}{l}x - y + 2 = 0\\x + y + 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 3\\y = - 1\end{array} \right.\)
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {1.1 + ( - 1).1} \right|}}{{\sqrt {{1^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {1^2}} }} = 0 \Rightarrow {d_1} \bot {d_2}\)
Vậy hai đường thẳng \({d_1}\) và \({d_2}\) vuông góc với nhau tại điểm có tọa độ \(( - 3; - 1)\)
b) Đường thẳng \({d_1}\) có phương trình tổng quát là: \({d_1}:2x - y + 1 = 0\)
Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ sau:
\(\left\{ \begin{array}{l}2x - y + 1 = 0\\x - 3y + 2 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - \frac{1}{5}\\y = \frac{3}{5}\end{array} \right.\)
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {2.\left( { - 1} \right) + 1.( - 3)} \right|}}{{\sqrt {{2^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = \frac{{\sqrt 2 }}{2} \Rightarrow \left( {{d_1},{d_2}} \right) = 45^\circ \)
Vậy hai đường thẳng \({d_1}\) và \({d_2}\) cắt nhau tại điểm có tọa độ \(\left( { - \frac{1}{5};\frac{3}{5}} \right)\) và góc giữa chúng là \(45^\circ \)
c) Đường thẳng \({d_1}\) và \({d_2}\) lần lượt có phương trình tổng quát là:
\({d_1}:3x + y - 11 = 0,{d_2}:x - 3y + 8 = 0\)
Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ sau:
\(\left\{ \begin{array}{l}3x + y - 11 = 0\\x - 3y + 8 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{5}{2}\\y = \frac{7}{2}\end{array} \right.\)
\(\cos \left( {{d_1},{d_2}} \right) = \frac{{\left| {3.1 + 1.( - 3)} \right|}}{{\sqrt {{3^2} + {1^2}} .\sqrt {{1^2} + {{\left( { - 3} \right)}^2}} }} = 0 \Rightarrow \left( {{d_1},{d_2}} \right) = 90^\circ \)
Vậy hai đường thẳng \({d_1}\) và \({d_2}\) vuông góc tại điểm có tọa độ \(\left( {\frac{5}{2};\frac{7}{2}} \right)\)

Ta thấy hai đường thẳng này song song, nên khoảng cách giữa chúng là khoảng cách từ một điểm bất kì từ đường thẳng này tới đường thẳng kia
Chọn điểm \(A\left( {0;4} \right) \in {d_2}\), suy ra \(d\left( {{d_1},{d_2}} \right) = d\left( {A,{d_1}} \right) = \frac{{\left| {4.0 - 3.4 + 2} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 2\)
Vậy khoảng cách giữa hai đường thẳng \({d_1}:4x - 3y + 2 = 0\) và \({d_2}:4x - 3y + 12 = 0\) là 2

a) \({d_1}\)và \({d_2}\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {1; - 1} \right),\overrightarrow {{n_2}} = \left( {1;1} \right)\)
Ta có \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 1.1 + ( - 1).1 = 0\) nên \(\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \)
Giải hệ phương trình \(\left\{ \begin{array}{l}x - y + 2 = 0\\x + y + 4 = 0\end{array} \right.\) ta được nghiệm \(\left\{ \begin{array}{l}x = - 3\\y = - 1\end{array} \right.\)
Suy ra hai đường thẳng \({d_1}\)và \({d_2}\) vuông góc và cắt nhau tại \(M\left( { - 3; - 1} \right)\)
b) \({d_1}\)và \({d_2}\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {5; - 2} \right),\overrightarrow {{n_2}} = \left( {5; - 2} \right)\)
\(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) trùng nhau nên hai vectơ pháp tuyến cùng phương. Suy ra \({d_1}\)và \({d_2}\)song song hoặc trùng nhau
Lấy điểm \(A(1;3)\) thuộc \({d_1}\), thay tọa độ của A vào phương trình \({d_2}\), ta được \(5.1 - 2.3 + 9 = 8 \ne 0\), suy ra A không thuộc đường thẳng \({d_2}\)
Vậy hai đường thẳng \({d_1}\)và \({d_2}\) song song
c) \({d_1}\)và \({d_2}\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {3;1} \right),\overrightarrow {{n_2}} = \left( {3;1} \right)\)
Suy ra hai vectơ pháp tuyến cùng phương. Suy ra \({d_1}\)và \({d_2}\)song song hoặc trùng nhau
Lấy điểm \(A(2;5)\) thuộc \({d_1}\), thay tọa độ của A vào phương trình \({d_2}\), ta được \(3.2 + 5 - 11 = 0\), suy ra A thuộc đường thẳng \({d_2}\)
Vậy hai đường thẳng \({d_1}\)và \({d_2}\) trùng nhau

a) \({d_1}\)và \({d_2}\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {1; - 5} \right),\overrightarrow {{n_2}} = \left( {10;2} \right)\)
Ta có \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 1.10 + ( - 5).2 = 0\) nên \(\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \)
Giải hệ phương trình \(\left\{ \begin{array}{l}x - 5y + 9 = 0\\10x + 2y + 7 = 10\end{array} \right.\) ta được nghiệm \(\left\{ \begin{array}{l}x = - \frac{3}{{52}}\\y = \frac{{93}}{{52}}\end{array} \right.\)
Suy ra hai đường thẳng \({d_1}\)và \({d_2}\) vuông góc và cắt nhau tại \(M\left( { - \frac{3}{{52}};\frac{{93}}{{52}}} \right)\)
b) \({d_1}\)và \({d_2}\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {3; - 4} \right),\overrightarrow {{n_2}} = \left( {3, - 4} \right)\)
\(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) trùng nhau nên hai vectơ pháp tuyến cùng phương. Suy ra \({d_1}\)và \({d_2}\)song song hoặc trùng nhau
Lấy điểm \(A(1;1)\) thuộc \({d_2}\), thay tọa độ của A vào phương trình \({d_1}\), ta được \(3.1 - 4.1 + 9 = 8 \ne 0\), suy ra A không thuộc đường thẳng \({d_1}\)
Vậy hai đường thẳng \({d_1}\)và \({d_2}\) song song
c) \({d_1}\)và \({d_2}\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {3; - 4} \right),\overrightarrow {{n_2}} = \left( {6; - 8} \right)\)
Ta có \({a_1}{b_2} - {a_2}{b_1} = 3.( - 8) - ( - 4).6 = 0\)suy ra hai vectơ pháp tuyến cùng phương. Suy ra \({d_1}\)và \({d_2}\)song song hoặc trùng nhau
Lấy điểm \(A(1;1)\) thuộc \({d_2}\), thay tọa độ của A vào phương trình \({d_1}\), ta được \(\left\{ \begin{array}{l}1 = 5 + 4t\\1 = 4 + 3t\end{array} \right. \Leftrightarrow t = - 1\), suy ra A thuộc đường thẳng \({d_1}\)
Vậy hai đường thẳng \({d_1}\) và \({d_2}\) trùng nhau

Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
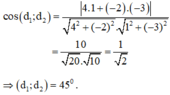

ta có vtpt của d1 : n=(1;2) và vtpt của d2: n'=(2;-1)
ta có cos\(\alpha\)=\(\dfrac{|\overrightarrow{n}\times\overrightarrow{n'}|}{\overrightarrow{|n|}\times|\overrightarrow{n'}|}\)=\(\dfrac{\left(1\times2\right)-\left(2\times1\right)}{\sqrt{1^2+2^2}\times\sqrt{\left(-1\right)^2+2^2}}\)=0
=>\(\alpha\)=\(90^0\)
Lời giải
Hệ số góc d1: k1=-1/2
hệ số góc d2: k2 =2
\(k_1.k_2=-1\) => d1 vuông góc với d2
góc d1 và d2 =90 độ
Áp dụng công thức cos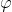 =
= 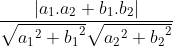
ta có cos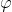 =
= 
=> cos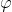 =
= 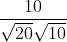 =
= 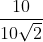 =
= 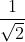 =>
=> 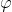 = 450
= 450
Vậy số đo góc giữa hai đường thẳng \(d_1\) và \(d_2\) là 45 độ.