OM
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PH
0
27 tháng 12 2021
\(2x^2+5xy+3y^2\\= 2x^2+2xy+3xy+3y^2\\= 2x\left(x+y\right)+3y\left(x+y\right)\\=\left(2x+3y\right)\left(x+y\right) \)
27 tháng 12 2021
2x^2-5xy-3y^2
= 2^x + xy - 6xy - 3y^2
= x(2x + y) - 3y(2x + y)
= (2x + y)(x - 3y)
LT
0
CM
22 tháng 8 2017
Đáp án B
Phương trình 7 x 2 - 12 x + 4 = 0 có a = 7; b' = -6; c = 4 suy ra:
Δ ' = ( b ' ) 2 - a c = ( - 6 ) 2 - 4 . 7 = 8 > 0
Nên phương trình có hai nghiệm phân biệt.
CM
27 tháng 1 2017
Phương trình 7x2 − 12x + 4 = 0
có a = 7;b’ = −6; c = 4 suy ra
Δ ' = b ' 2 − a c = (−6)2 – 4.7 = 8 > 0
Nên phương trình có hai nghiệm phân biệt
Đáp án cần chọn là: B
CM
28 tháng 8 2018
Gọi hai nghiệm của phương trình là x1; x2.
Theo định lý Vi-et ta có: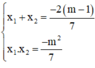 
Khi đó:
CM
16 tháng 1 2017
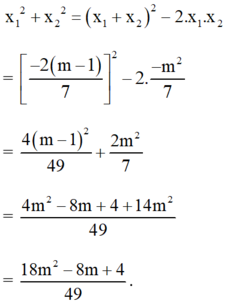
a) Ta có: a = 7, b= 2(m-1), c = - m 2
Suy ra: Δ ' = ( m - 1 ) 2 + 7 m 2
Do ( m - 1 ) 2 ≥ 0 mọi m và m 2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
b) Gọi hai nghiệm của phương trình là x 1 ; x 2 .
Theo định lý Vi-et ta có: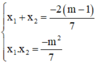 
Khi đó:
CM
6 tháng 11 2017
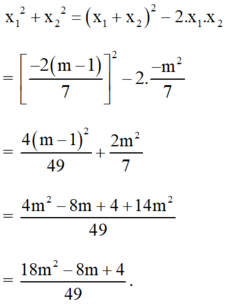
Ta có: a = 7, b= 2(m-1), c = - m2
Suy ra: Δ' = (m - 1)2 + 7m2
Do (m-1)2 ≥ 0 mọi m và m2 ≥ 0 mọi m
=> ∆’≥ 0 với mọi giá trị của m.
Do đó phương trình có nghiệm với mọi giá trị của m.
19 tháng 7 2021
\(x^4+y^4=3y^2+1\Leftrightarrow-y^4+3y^2+1=x^4\ge0\)
\(\Rightarrow-y^4+3y^2+1\ge0\Rightarrow\frac{3-\sqrt{13}}{2}\le y^2\le\frac{3+\sqrt{13}}{2}\)
Mà \(y\in Z\Rightarrow y^2\)là số chính phương \(\Rightarrow y^2=0;1\)
*\(y^2=0\Rightarrow x^4=1\Rightarrow x=-1;1\)
*\(y^2=1\Rightarrow x^4+1=3+1\Rightarrow x^4=3\Rightarrow x\notin Z\)
Vậy phương trình có nghiệm nguyên \(\left(-1;0\right),\left(1;0\right)\)
Ta có:\(7⋮7\Rightarrow7x^2⋮7;714⋮7\)
\(\Rightarrow3y^2⋮7\)
Mà \(\left(3,7\right)=1\Rightarrow y^2⋮7\Rightarrow y^2⋮49\)(tính chất số chính phương)
Lại có:\(3y^2\le714\Rightarrow y^2\le238\)
\(\Rightarrow y^2\in\left\{49;196\right\}\)vì y là số chính phương
Với \(y^2=49\Rightarrow\orbr{\begin{cases}y=7\Rightarrow x=\pm9\\y=-7\Rightarrow7x^2=567\Rightarrow x^2=81\Rightarrow x=\pm9\end{cases}}\)
tương tự với \(y^2=196\)nhé
Đệ hãu giải thích tính chất scp