NT
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
12 tháng 5 2022
Ta có \(x^2-7x+8=0\Leftrightarrow x^2-\dfrac{2.7}{2}x+8=0\)
\(\Leftrightarrow x^2-7x+\dfrac{49}{4}-\dfrac{49}{4}+8=0\Leftrightarrow\left(x-\dfrac{7}{2}\right)^2-\dfrac{17}{4}=0\)
\(\left[{}\begin{matrix}x-\dfrac{7}{2}=\dfrac{\sqrt{17}}{2}\\x-\dfrac{7}{2}=-\dfrac{\sqrt{17}}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{17}+7}{2}\\x=\dfrac{-\sqrt{17}+7}{2}\end{matrix}\right.\)
12 tháng 5 2022
Đặt \(x^2-7x+8=0\)
\(\Delta=\left(-7\right)^2-4\cdot1\cdot8=17>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{7-\sqrt{17}}{2}\\x_2=\dfrac{7+\sqrt{17}}{2}\end{matrix}\right.\)
12 tháng 5 2022
Đặt \(x^2-7x+8=0\)
\(\Delta=\left(-7\right)^2-4\cdot1\cdot8=17>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{7-\sqrt{17}}{2}\\x_2=\dfrac{7+\sqrt{17}}{2}\end{matrix}\right.\)
13 tháng 5 2022
Đặt \(-16x^2+7x+18=0\)
\(\text{Δ}=7^2-4\cdot\left(-16\right)\cdot18=1201>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-7-\sqrt{1201}}{-32}=\dfrac{7+\sqrt{1201}}{32}\\x_2=\dfrac{7-\sqrt{1201}}{32}\end{matrix}\right.\)
16 tháng 4 2018
a) Sắp xếp theo lũy thừa giảm dần
P(x)=x^5−3x^2+7x^4−9x^3+x^2−1/4x
=x^5+7x^4−9x^3−3x^2+x^2−1/4x
=x^5+7x^4−9x^3−2x^2−1/4x
Q(x)=5x^4−x^5+x^2−2x^3+3x^2−1/4
=−x^5+5x^4−2x^3+x^2+3x^2−1/4
=−x^5+5x^4−2x^3+4x^2−1/4
b)
P(x)+Q(x)
=(x^5+7x^4−9x^3−2x^2−1/4^x)+(−x^5+5x^4−2x^3+4x^2−1/4)
=x^5+7x^4−9x^3−2x^2−1/4x−x^5+5x^4−2x^3+4x^2−1/4
=(x^5−x^5)+(7x^4+5x^4)+(−9x^3−2x^3)+(−2x^2+4x^2)−1/4x−1/4
=12x^4−11x^3+2x^2−1/4x−1/4
P(x)−Q(x)
=(x^5+7x^4−9x^3−2x^2−1/4x)−(−x^5+5x^4−2x^3+4x^2−1/4)
=x^5+7x^4−9x^3−2x^2−1/4x+x^5−5x^4+2x^3−4x^2+1/4
=(x^5+x^5)+(7x^4−5x^4)+(−9x^3+2x^3)+(−2x^2−4x^2)−1/4x+1/4
=2x5+2x4−7x3−6x2−1/4x−1/4
c) Ta có
P(0)=0^5+7.0^4−9.0^3−2.0^2−1/4.0
⇒x=0là nghiệm của P(x).
Q(0)=−0^5+5.0^4−2.0^3+4.0^2−1/4=−1/4≠0
⇒x=0không phải là nghiệm của Q(x).
7 tháng 7 2020
Cho 2 đa thức: f(x)= 9 - x5 + 4x - 2x3 + x2 - 7x4
g(x)= x5 - 9 + 2x2 + 7x4 + 2x3 - 3x
a) Sắp sếp các đa thức trên theo luỹ thừa giảm dần của biến
f(x)= 9 - x5 + 4x - 2x3 + x2 - 7x4
f(x) = -x5 - 7x4 - 2x3 + x2 + 4x + 9
g(x)= x5 - 9 + 2x2 + 7x4 + 2x3 - 3x
g(x) = x5 + 7x4 + 2x3 + 2x2 - 3x - 9
b) Tìm bậc, hệ số cao nhất, hệ số tự do của đa thức f(x); g(x)
f(x) = -x5 - 7x4 - 2x3 + x2 + 4x + 9
+ Bậc : 5 _ hệ số cao nhất : -1 _ hệ số tự do : 9
g(x) = x5 + 7x4 + 2x3 + 2x2 - 3x - 9
+ Bậc : 5_ hệ số cao nhất : 1 _ hệ số tự do : -9
c) Tính f(x) + g(x); f(x) - g(x)
f( x) + g(x) = ( -x5 - 7x4 - 2x3 + x2 + 4x + 9 ) +( x5 + 7x4 + 2x3 + 2x2 - 3x - 9 )
= -x5 - 7x4 - 2x3 + x2 + 4x + 9 + x5 + 7x4 + 2x3 + 2x2 - 3x - 9
= ( -x5 + x5 ) + ( -7x4 + 7x4 ) + ( -2x3 + 2x3 ) + ( x2 + 2x2 ) + ( 4x -3x ) + ( 9 - 9 )
= 3x2 + x
f( x) - g(x) = ( -x5 - 7x4 - 2x3 + x2 + 4x + 9 ) - ( x5 + 7x4 + 2x3 + 2x2 - 3x - 9 )
= -x5 - 7x4 - 2x3 + x2 + 4x + 9 - x5 - 7x4 - 2x3 - 2x2 + 3x + 9
= ( -x5 - x5 ) + ( -7x4 - 7x4 ) + ( -2x3 - 2x3 ) + ( x2 - 2x2 ) + ( 4x + 3x ) + ( 9 + 9 )
= -2x5 - 14x4 - 2x3 -x2 + 7x + 18
19 tháng 3 2018
a, \(P\left(x\right)=0\)
\(\Leftrightarrow5x-4=0\)
\(\Leftrightarrow5x=4\)
\(\Leftrightarrow x=\dfrac{4}{5}\)
Vậy ...
b/ \(Q\left(x\right)=0\)
\(\Leftrightarrow x^2-7x=0\)
\(\Leftrightarrow x\left(x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-7=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=7\end{matrix}\right.\)
Vậy ..
HA
10 tháng 6 2020
\(f\left(x\right)=x2-7x+6\)
ta có f(x)=0
hay\(x2-7x+6=0\)
\(\Leftrightarrow x2-7x=-6\)
\(\Leftrightarrow x\left(-5\right)=-6\)
\(\Leftrightarrow x=\frac{6}{5}\)
vậy nghiệm của đa thức f(x) là 6/5
10 tháng 6 2020
\(f\left(x\right)=x^2-7x+6\)
\(f\left(x\right)=0\Leftrightarrow x^2-7x+6=0\)
\(\Leftrightarrow x^2-x-6x+6=0\)
\(\Leftrightarrow x.\left(x-1\right)-6.\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right).\left(x-6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x-6=0\end{cases}\Leftrightarrow}\orbr{\begin{cases}z=1\\x=6\end{cases}}\)
Vậy phương trình có 2 nghiệm \(x=\left\{1,6\right\}\)
C
14 tháng 3 2023
`x^2 - 3x = 0`
`<=> x.(x-3)=0`
`<=> x = 0` hoặc `x-3=0`
`<=> x = 0 ` hoặc `x = 3`
Vậy `S = { 0;3}`
`2x^2 + 5x = 0`
`<=> x.(2x + 5)=0`
`<=> x = 0` hoặc `2x+5=0`
`<=> x = 0` hoặc `2x= -5`
`<=> x = 0` hoặc `x = -5/2`
Vậy `S = {0; -5/2}`
14 tháng 3 2023
\(a,x^2-3x=0\\ x\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\\ b,2x^2+5x=0\\ x\left(2x+5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\2x+5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{2}\end{matrix}\right.\)
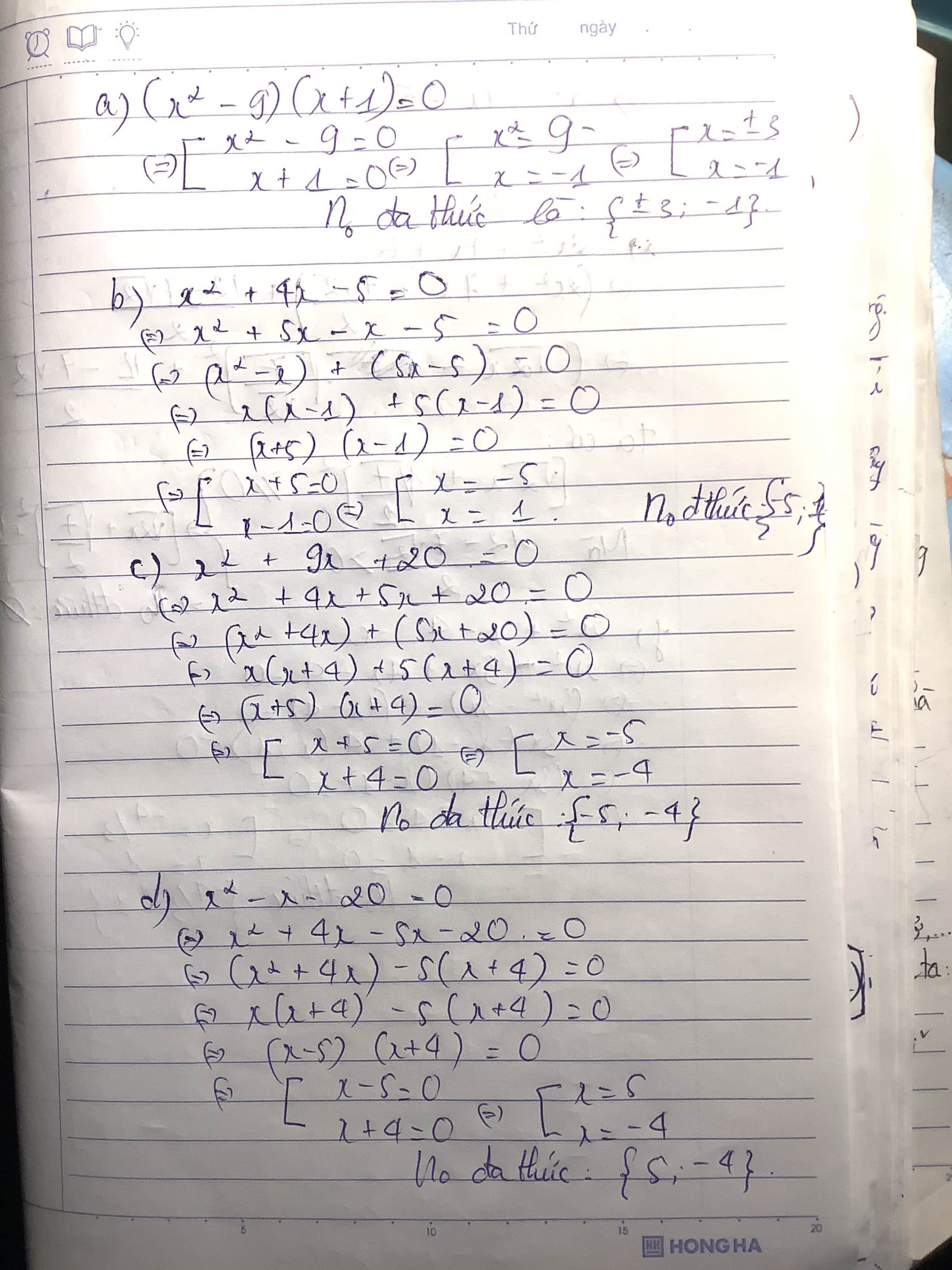
Ta có : \(x^2+5x=0\)
\(\Leftrightarrow x.\left(x+5\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x+5=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=-5\end{cases}}\)
Vậy đa thức trên có 2 nghiệm là x=0 hoặc x=-5
Ta có : \(x^2+7x+12=0\)
\(\Leftrightarrow\left(x+3,5\right)^2-0,25=0\)
\(\Leftrightarrow\left(x+3,5\right)^2=0,25\)
\(\Leftrightarrow x+3,5=0,5\)
\(\Leftrightarrow x=-3\)
Vậy đa thức trên có 1 nghiệm là x=-3
1) x2 + 5x
Đặt x2 + 5x = 0
=> x.(x + 5) = 0
=> \(\orbr{\begin{cases}x=0\\x+5=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=-5\end{cases}}\). Vậy x \(\in\){0 , -5} là nghiệm của x2 + 5x
2) x2 + 7x + 12
Đặt x2 + 7x + 12 = 0
=> x2 + 3x + 4x + 12 = 0
=> x.(x + 3) + 4(x + 3) = 0
=> (x + 3)(x + 4) = 0
\(\Rightarrow\orbr{\begin{cases}x+3=0\\x+4=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-3\\x=-4\end{cases}}\).Vậy x \(\in\){-3 , -4} là nghiệm của x2 + 7x + 12
- Đúng 100%