K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
9 tháng 5 2017
Cách 1: Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
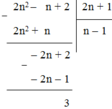
2n2 – n + 2 chia hết cho 2n + 1
⇔ 3 ⋮ (2n + 1) hay (2n + 1) ∈ Ư(3)
⇔ 2n + 1 ∈ {±1; ±3}
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Cách 2:
Ta có:
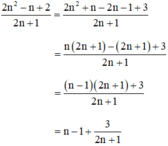
2n2 – n + 2 chia hết cho 2n + 1
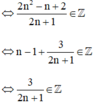
⇔ 2n + 1 ∈ Ư(3) = {±1; ± 3}.
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Chú ý: Đa thức A chia hết cho đa thức B khi phần dư của phép chia bằng 0.
DF
1
HH
2 tháng 7 2020
Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
2n2 – n + 2 chia hết cho 2n + 1
<=> 3 \(⋮\)( 2n + 1 ) hay ( 2n + 1 ) \(\in\) Ư(3)
<=> 2n + 1 \(\in\) {\(\pm\)1; \(\pm\)3 }
+ 2n + 1 = 1 <=> 2n = 0 <=> n = 0
+ 2n + 1 = -1 <=> 2n = -2 <=> n = -1
+ 2n + 1 = 3 <=> 2n = 2 <=> n = 1
+ 2n + 1 = -3 <=> 2n = -4 <=> n = -2.
Vậy n \(\in\) { -2 ; -1 ; 0 ; 1 }
17 tháng 12 2018
\(2n^2-n+2⋮2n+1\)
\(2n^2+n-2n-1+3⋮2n+1\)
\(n\left(2n+1\right)-\left(2n+1\right)+3⋮2n+1\)
\(\left(2n+1\right)\left(n-1\right)+3⋮2n+1\)
Vì \(\left(2n+1\right)\left(n-1\right)⋮2n+1\)
\(\Rightarrow3⋮2n+1\)
\(\Rightarrow2n+1\inƯ\left(3\right)=\left\{1;3;-1;-3\right\}\)
\(\Rightarrow n\in\left\{0;1;-1;-2\right\}\)
Vậy.........
CD
1
4 tháng 11 2015
2n2+5n-1=n(2n-1)+6n-1
=n(2n-1)+3(2n-1)+2
do 2n2+5n-1 chia hết cho 2n-1 => 2 chia hết cho 2n-1
=> 2n-1 thuộc tập ước của 2 là 1;2
=> n=1 (TM) n=1,5 (loại)
3 tháng 7 2023
1:
2n^2+5n-1 chia hết cho 2n-1
=>2n^2-n+6n-3+2 chia hết cho 2n-1
=>2n-1 thuộc {1;-1;2;-2}
mà n nguyên
nên n=1 hoặc n=0
2:
a: A=n(n+1)(n+2)
Vì n;n+1;n+2 là 3 số liên tiếp
nên A=n(n+1)(n+2) chia hết cho 3!=6
b: B=(2n-1)[(2n-1)^2-1]
=(2n-1)(2n-2)*2n
=4n(n-1)(2n-1)
Vì n;n-1 là hai số nguyên liên tiếp
nên n(n-1) chia hết cho 2
=>B chia hết cho 8
c: C=n^2+14n+49-n^2+10n-25=24n+24=24(n+1) chia hết cho 24
17 tháng 1 2017
(Chỉ là chia đa thức thôi mà!)
Anh giải câu b thôi, mấy câu còn lại tự làm nha.
\(2n^3+n^2+7n+1=\left(2n-1\right)\left(n^2+n+4\right)+5\)
Suy ra \(\frac{2n^3+n^2+7n+1}{2n-1}=n^2+n+4+\frac{5}{2n-1}\)
Để vế trái nguyên thì \(2n-1\) là ước của \(5\). Giải được \(n=-2,0,1,3\)
15 tháng 10 2015
Ta có :
\(2n^2-n+2=-n.\left(-2n+1\right)+2\)
Vì -2n + 1 chia hết cho 2n + 1 nên -n.(-2n + 1) cũng chia hết cho 2n + 1
=> 2 chia hết cho 2n + 1
Vì n thuộc Z nên 2n + 1 thuộc {-2;-1;1;2}
=> n thuộc {-1; 0}
PN
15 tháng 11 2015
Ta có: \(2n^2-n-1=2n^2+3n-4n-6+5=n\left(2n+3\right)-2\left(2n+3\right)+5\)
Vì \(n\left(2n+3\right)\)và \(-2\left(2n+3\right)\)chia hết cho \(2n+3\) nên để \(2n^2-n-1\)chia hết cho \(2n+3\) thì \(5\)phải chia hết cho \(2n+3\), tức là \(2n+3\inƯ\left(5\right)=\left\{1;-1;5;-5\right\}\)
Với \(2n+3=1\)thì \(n=-1\)
Với \(2n+3=-1\) thì \(n=-2\)
Với \(2n+3=5\)thì \(n=1\)
Với \(2n+3=-5\) thì \(n=-4\)
Vậy, để đa thức \(2n^2-n-1\) chia hết cho đa thức \(2n+3\) thì \(n=\left\{-2;-1;1;-4\right\}\) và \(n\in Z\)
TÌM n thuộc Z để 2n2 – n + 2 chia hết 2n + 1.
Phép chia hết khi : 2n + 1 có giá trị là U(3) ={ ±1; ±3}
Vậy : n = 0, – 1, 1, – 2