K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LM
3
LM
22 tháng 1 2016
a) 3n + 2 chia hết cho n - 1
\(\Rightarrow\) 3n - 3 + 5 chia hết cho n - 1
\(\Rightarrow\) 3(n - 1) + 5 chia hết cho n - 1
\(\Rightarrow\) 5 chia hết cho n - 1
\(\Rightarrow\) n - 1 \(\in\) Ư(5) = {-1; 1; -5; 5}
\(\Rightarrow\) n \(\in\) {0; 2; -4; 6}
b) 3n + 24 chia hết cho n - 4
\(\Rightarrow\) 3n - 12 + 36 chia hết cho n - 4
\(\Rightarrow\) 3(n - 4) + 36 chia hết cho n - 4
\(\Rightarrow\) 36 chia hết cho n - 4
\(\Rightarrow\) n - 4 \(\in\) Ư(36) = {-1; 1; -2; 2; -3; 3; -4; 4; -6; 6; -9; 9; -12; 12; -18; 18; -36; 36}
\(\Rightarrow\) n \(\in\) {-3; 5; 4; 6; -1; 7; 0; 8; -2; 10; -5; 13; -8; 16; -14; 22; -32; 40}
c) 3n + 5 chia hết cho n + 1
\(\Rightarrow\) 3n + 3 + 2 chia hết cho n + 1
\(\Rightarrow\) 3(n + 1) + 2 chia hết cho n + 1
\(\Rightarrow\) 2 chia hết cho n + 1
\(\Rightarrow\) n + 1 \(\in\) Ư(2) = {-1; 1; -2; 2}
\(\Rightarrow\) n \(\in\) {0; 2; -1; 3}
MV
19 tháng 2 2016
11,
a, 4x-3\(\vdots\) x-2 1
x-2\(\vdots\) x-2\(\Rightarrow\) 4(x-2)\(\vdots\) x-2\(\Rightarrow\) 4x-8\(\vdots\) x-2 2
Từ 1 và 2 ta có:
(4x-3)-(4x-8)\(\vdots\) x-2
\(\Rightarrow\) 4x-3-4x+8\(\vdots\) x-2
\(\Rightarrow\) 5 \(\vdots\) x-2
\(\Rightarrow\) x-2\(\in\) Ư(5)
\(\Rightarrow\) x-2\(\in\){-5;-1;1;5}
\(\Rightarrow\) x\(\in\) {-3;1;3;7}
Vậy......
Phần b và c làm tương tự như phần a pn nhé! 
NV
4 tháng 2 2016
Có: \(\frac{4n+3}{n-2}=4+\frac{11}{n-2}\)
Để (4n + 3) chia hết cho (n - 2) thì (n - 2) \(\in\) Ư(11) = {1;-1;11;-11}
n - 2 = 1 => n = 3 (nhận)
n - 2 = -1 => n = 1 (n)
n - 2 = 11 => n = 13 (n)
n - 2 = -11 => n = -9 (n)
Vậy n = {3;1;13;-9}
4 tháng 2 2016
4n + 3 ⋮ n - 2 <=> 4.( n - 2 ) + 11 ⋮ n - 2
Vì n - 2 ⋮ n - 2 . Để 4.( n - 2 ) + 11 ⋮ n - 2 <=> 11 ⋮ n - 2 => n - 2 ∈ Ư ( 11 ) = { + 1 ; + 11 }
=> n ∈ { - 9 ; 1 ; 3 ; 13 }
Ta có bảng sau :
| n - 2 | 1 | - 1 | 11 | - 11 |
| n | 3 | 1 | 13 | - 9 |
14 tháng 1 2016
Ta có : n + 3 : n -1
=> n - 1 + 4 : n - 1
=> 4 chia hết cho n - 1 ( Vì n - 1 chia hết cho n -1)
=> n - 1 \(\in\) Ư (4)
=> n - 1 \(\in\) {1 ; 2 ; 4 ; -1 ; -2 ; -4}
TH1: n - 1 = 1 TH4 : n - 1 = - 1
=> n = 2 => n = 0
TH2 : n - 1 = 2 TH5 : n - 1 = -2
=> n = 3 => n = -1
TH3 : n - 1 = 4 TH6: n - 1 = -4
=> n = 5 => n = -3
Vậy n \(\in\) {2 ; 3 ; 5 ; 0 ; -1 ; - 3}
TK
30 tháng 12 2016
Để n+3 chia hết cho n-1
Thì n+4-1 chia hết cho n-1
Mà n-1 chia hết cho n-1
Nên suy ra 4 phải chia hết cho n-1
Khi n-1 thuộc Ư(4)={1;-1;2;-2;4;-4}
Ta có bảng sau:
| n-1 | 1 | 2 | 4 | -1 | -2 | -4 |
| n | 2 | 3 | 5 | 0 | -1 |
-3 |
Vậy n=2 ; n=3 ;n=5 ;n= 0 ; n=-1 hoặc n= -3
10 tháng 4 2016
vì 3n^2 chia hết cho 3 nên để A chia hết cho 3 thì ta CM
n^3+2n=n*(n*n+2) vì n là số nguyên nên n có dạng 3k; 3k+1;3k+2(k thuộc Z)
nếu n=3k thì n*(n*n+2) luôn luôn chia hết cho 3
nếu n=3k+1 thì n*n=(3k+1)*(3k+1)=9k^2+3k+3k+1 chia 3 dư 1 nên n*n+2 luôn luôn chia hết cho 3
nếu n=3k+2 thì n*n=(3k+2)*(3k+2)=9k^2+6k+6k+4 chia 3 dư 1 nên n*n+2 luôn luôn chia hết cho 3
vậy biểu thức trên luôn luôn chia hết cho 3 với mọi n thuộcZ
10 tháng 4 2016
câu b)để A chia hết cho 15 thì n^3+3n^2+2n phải chia hết cho 3;5(vì ƯCLN(3;5)=1)
Mà theo câu a thì A luôn luôn chia hết cho 3 với n thuộc Z
nên ta chỉ cần tìm giá trị của n để A chia hết cho5
để A chia hết cho 5 thì n^3 phải chia hết cho 5;3n^2 phải chia hết cho 5;2n phải chia hết cho 5
nên n phải chia hết cho 5(vì ƯCLN(3;5)=1;ƯCLN(2;5)=1 nên n^3;n^2;n phải chia hết cho 5 nên ta suy ra n phải chia hết cho 5)
mà 1<n<10 nên n=5(n là số nguyên dương)
vậy giá trị của n thỏa mãn đề bài là 5
CM
23 tháng 10 2018
Đáp án A
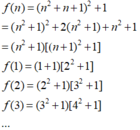
= > U n = ( 1 2 + 1 ) ( 2 2 + 1 ) . ( 3 2 + 1 ) ( 4 2 + 1 ) ... [ ( 2 n − 1 ) 2 + 1 ] [ ( 2 n ) 2 + 1 ] ( 2 2 + 1 ) ( 3 2 + 1 ) . ( 4 2 + 1 ) ( 5 2 + 1 ) ... [( 2 n ) 2 + 1 ] [ ( 2 n + 1 ) 2 + 1 ] = > U n = 2 ( 2 n + 1 ) 2 + 1
NN
7 tháng 3 2016
Ta có : \(\frac{8n+3}{2n-1}=4+\frac{7}{2n-1}\)
nên để \(8n+3\) chia hết cho \(2n-1\) thì \(7\)phải chia hết cho \(2n-1\), tức \(n\ne\frac{1}{2}\); \(n=1;n=4;\)
Vậy tập hơp các số nguyên thỏa mãn ycbt là \(n\in\left\{1;4\right\}\)
8 tháng 3 2016
Để 8n + 3 chia hết cho 2n - 1 <=> \(\frac{8n+3}{2n-1}\) là số nguyên
Ta có :\(\frac{8n+3}{2n-1}=\frac{4\left(2n-1\right)+7}{2n-1}=\frac{4\left(2n-1\right)}{2n-1}+\frac{7}{2n-1}=4+\frac{7}{2n-1}\)
Để \(4+\frac{7}{2n-1}\) là số nguyên <=> \(\frac{7}{2n-1}\) là số nguyên
=> 2n - 1 \(\in\) Ư ( 7 ) => Ư ( 7 ) = { - 7 ; - 1 ; 1 ; 7 }
Ta có : 2n - 1 = - 7 <=> 2n = - 6 => n = - 3 ( TM )
2n - 1 = - 1 <=> 2n = 0 => n = 0 ( TM )
2n - 1 = 1 <=> 2n = 2 => n = 1 ( TM )
2n - 1 = 7 <=> 2n = 8 => n = 4 ( TM )
Vậy n \(\in\) { - 3 ; 0 ; 1 ; 4 }
L
24 tháng 4 2016
\(n-3\text{⋮}n-3\)
\(\Rightarrow n\left(n-3\right)\text{⋮}n-3\)
\(\Rightarrow n^2-3n\text{⋮}n-3\)
Mà \(n^2-3\text{⋮}n-3\)
\(\Rightarrow\left(n^2-3\right)-\left(n^2-3n\right)\text{⋮}n-3\)
\(\Rightarrow3n-3\text{⋮}n-3\)
Lại có:\(n-3\text{⋮}3\Rightarrow3\left(n-3\right)\text{⋮}n-3\)
\(\Rightarrow3n-9\text{⋮}3\)
Mà \(3n-3\text{⋮}n-3\)
\(\Rightarrow\left(3n-3\right)-\left(3n-9\right)\text{⋮}n-3\)
\(6\text{⋮}n-3\)
\(\Rightarrow n-3\inƯ\left(6\right)=\left\{-6;-3;-2;-1;1;2;3;6\right\}\)
\(\Rightarrow n\in\left\{-3;0;1;2;4;5;6;9\right\}\)
Vậy \(n\in\left\{-3;0;1;2;4;5;6;9\right\}\)
22 tháng 4 2016
Ta có :
n2 - 3 chia hết cho n - 3
<=> n.n - 3 chia hết cho n -3
<=> 2n - 3 chia hết cho n - 3
<=> 2n - 6 + 3 chia hết cho n - 3
<=> 2.(n-3) + 3 chia hết cho n - 3
<=> 3 chia hết cho - 3
<=> n - 3 \(\in\) Ư(3) = {\(\pm\)1;\(\pm\)3}
<=> \(\begin{cases}n-3=1\Rightarrow n=4\\n-3=-1\Rightarrow n=2\\n-3=3\Rightarrow n=6\\n-3=-3\Rightarrow n=0\end{cases}\)
Vây n \(\in\) {4;2;6;0}
Ta có :
n2 - n - 1 = n.(n - 1) - 1 chia hết cho (n - 1)
Do n.(n - 1) chia hết cho (n - 1) nên suy ra 1 chia hết hết cho (n - 1)
nên (n - 1) \(\in\) Ư(1) = {-1; 1}
\(\Leftrightarrow\) n \(\in\) {0; 2}
Theo đề, ta có :
\(\left(n^2-n-1\right)⋮\left(n-1\right)\)
<=> n( n - 1) -1 \(⋮\) ( n - 1)
<=> 1 \(⋮\) ( n - 1) ( vì n( n - 1) \(⋮\) ( n - 1)
<=> \(\left(n-1\right)\inƯ\left(1\right)=\left\{\pm1\right\}\)
\(n-1=1\Rightarrow n=2\)
\(n-1=-1\Rightarrow n=0\)
Vậy \(n\in\left\{0;2\right\}\)thì (n2 - n - 1) \(⋮\) (n - 1)