K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
0
NV
1
NV
0
NN
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
2 tháng 10 2023
A = 2 + 22+...+ 249 + 250
2A = 22 +...+ 249 + 250 + 251
2A - A = 251 - 2
A = 251 - 2
A + 1 = 251 - 2 + 1 = 251 - 1 (là số lẻ)
\(2^{2n^2+1}\) là số chẵn với \(\forall\) n
Vậy A = 2 + 22 + ...+ 250 \(\ne\) \(2^{2n^2+1}\) \(\forall\) n
Vậy n \(\in\) \(\varnothing\)
27 tháng 1 2018
b) n + 3 \(⋮\) n - 1 <=> (n - 1) + 4 \(⋮\) n - 1
=> 4 \(⋮\) n - 1 (vì n - 1 \(⋮\) n - 1)
=> n - 1 ∈ Ư(4) = {±1; ±2; ±4}
Lập bảng giá trị:
| n - 1 | 1 | -1 | 2 | -2 | 4 | -4 |
| n | 2 | 0 | 3 | -1 | 5 | -3 |
Vậy n ∈ {2; 0; 3; -1; 5; -3}
23 tháng 7 2023
a: Số số hạng là 100-50+1=51 số
Tổng là (100+50)*51/2=51*75=3825
b: Số số hạng là (223-21):2+1=102(số)
Tổng là (223+21)*102/2=12444
c: Số số hạng là (72-12):4+1=16(số)
Tổng là (72+12)*16/2=672
d: Số số hạng là (124-4):6+1=21(số)
Tổng là (124+4)*21/2=1344
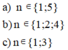
a) n = 6
b) không tồn tại n
a) 50 <2^n <100
50 < 2^6
2^6 < 100
=> n = 6 duy nhất
b)50 < 7^n < 2500
7^2 < 50 < 7^3
7^4 < 50^2 = 2500
n = 3 và 4