Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có d ∩ d ’ ⇔ m – 3 ≠ 2 ⇔ m ≠ 5
Xét phương trình hoành độ của d’ và d’’:
2 x – 1 = ( m – 3 ) x + 2 ⇔ ( m – 5 ) x = − 3 ⇔ x = − 3 m − 5
y = − 6 m − 5 − 1 = − m − 1 m − 5
Theo đề bài x . y > 0 ⇔ − 3 m − 5 . − m − 1 m − 5 > 0 ⇔ 3 m + 1 m − 5 2 > 0
Mà ( m – 5 ) 2 > 0 . ∀ m ≠ 5
Suy ra m > −1
Kết hợp điều kiện ta có: m > − 1 m ≠ 5
Đáp án cần chọn là: B
Đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 1 - 2 2 nên ta có n = 1 - 2
Đường thẳng (d) cắt trục hoành tại điểm có hoành độ bằng 2 + 2 nên ta có:
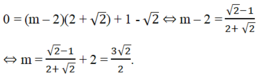
Trả lời: Khi n = 1 -
2
và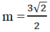 
thì đường thẳng (d) cắt trục tung tại điểm có tung độ bằng 1 -
2
và cắt trục hoành tại điểm có hoành độ 2 +
2
PTHĐGĐ là:
x^2-2x-m=0(1)
Thay x=-1 vào (1), ta được
(-1)^2-2*(-1)-m=0
=>1+2-m=0
=>m=3
x1+x2=2
=>x2=2-(-1)=3
=>A(-1;1); B(3;9)
a: Vì (d) đi qua hai điểm (0;5) và (-2;0) nên ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot0+b=5\\-2a+b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=5\\-2a=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=5\\a=\dfrac{5}{2}\end{matrix}\right.\)
a: f(2)=2^2=4
thay x=2 và y=4 vào (d), ta được:
4(m-1)+m=4
=>5m-4=4
=>m=8/5
b: PTHĐGĐ là;
x^2-2(m-1)x-m=0
Để (P) cắt (d) tại hai điểm nằm về hai phía so với trục tung thì -m<0
=>m>0
x1^2+2(m-1)x2=6
=>x1^2+x2(x1+x2)=6
=>x1^2+x2^2+x1x2=6
=>(x1+x2)^2-x1x2=6
=>(2m-2)^2-(-m)-6=0
=>4m^2-8m+4+m-6=0
=>m=2(nhận) hoặc m=-1/4(loại)
b1 tìm điều kiện để (d1) cắt (d2) m khác 1
b2 lập phương trình hoành độ (m+1)x+2=2x+1 Tìm x=-1/(m-1) \(\Rightarrow y=\frac{m-3}{m-1}\)
b3 Để d1 cắt d2 tại 1 điểm có hoành độ và tung độ trái dấu \(\left(\frac{-1}{m-1}\right)\left(\frac{m-3}{m-1}\right)< 0\). Tìm m (m>3)
b4 Kết luận