tìm m để với mọi x \(-1\le\dfrac{x^2+5x+m}{2x^2-3x+2}< 7\)

KH

Kimian Hajan Ruventaren

20 tháng 3 2021

Xác định m để với mọi m ta có

\(-1\le\dfrac{x^2+5x+m}{2x^2-3x+2}< 7\)

#Toán lớp 10

0

NG

Nguyễn Gia Bích

31 tháng 3 2020

xác định m để với mọi x ta có: \(1\le\frac{x^2+5x+m}{2x^2-3x+2}< 7\)

#Toán lớp 10

0

TK

Trần Khánh Linh

9 tháng 6 2021

Xác đinh ̣ m để với moi ̣ x ta có \(-1\le\dfrac{x^2+5x+m}{2x^2-3x+2}< 7\)

#Toán lớp 10

1

LT

Lê Thị Thục Hiền

9 tháng 6 2021

Đk: \(x\in R\)

Có \(2x^2-3x+2>0;\forall x\)

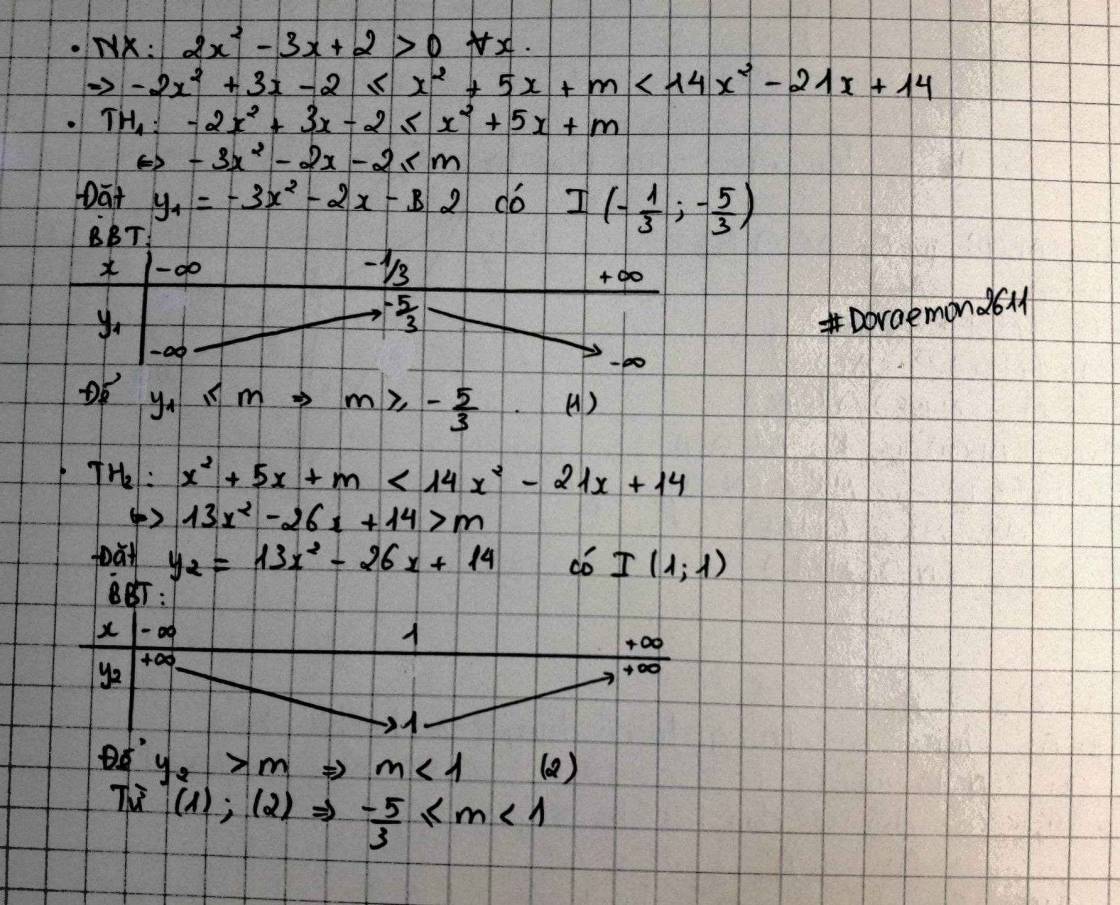
\(-1\le\dfrac{x^2+5x+m}{2x^2-3x+2}< 7\) với \(\forall x\)\(\Leftrightarrow-2x^2+3x-2\le x^2+5x+m< 14x^2-21x+14\) với mọi x

\(\Leftrightarrow\left\{{}\begin{matrix}3x^2+2x+m+2\ge0;\forall x\left(1\right)\\13x^2-26x+14-m>0;\forall x\left(2\right)\end{matrix}\right.\)

Từ \(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}a=3>0\left(lđ\right)\\\Delta\le0\end{matrix}\right.\)\(\Leftrightarrow4-4.3\left(m+2\right)\le0\)\(\Leftrightarrow-20-12m\le0\)\(\Leftrightarrow m\ge\dfrac{-5}{3}\)

Từ \(\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}a=13>0\left(lđ\right)\\\Delta< 0\end{matrix}\right.\)\(\Leftrightarrow m< 1\)

Vậy \(-\dfrac{5}{3}\le m< 1\)

Đúng(1)

TN

Thảo Nguyên

5 tháng 3 2021

Câu 1: Tìm m để biểu thức sau luôn âm: (m-4)x²+ (m+1)x + 2m-1

Câu 2: Tìm m để bất phương trình sau có nghiệm đúng với mọi x:

a/ \(\dfrac{3x^2-5x+4}{\left(m-4\right)x^2+\left(1+m\right)x+2m-1}>0\)

b/ \(-4< \dfrac{2x^2+mx-4}{-x^2+x-1}< 6\)

GIÚP MÌNH VỚI Ạ!!!

#Toán lớp 10

3

HP

Hồng Phúc

5 tháng 3 2021

2.

b, \(-4< \dfrac{2x^2+mx-4}{-x^2+x-1}< 6\)

\(\Leftrightarrow\left\{{}\begin{matrix}-4< \dfrac{2x^2+mx-4}{-x^2+x-1}\left(1\right)\\\dfrac{2x^2+mx-4}{-x^2+x-1}< 6\left(2\right)\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow4\left(x^2-x+1\right)>2x^2+mx-4\)

\(\Leftrightarrow2x^2-\left(m+4\right)x+8>0\)

Yêu cầu bài toán thỏa mãn khi \(\Delta=m^2+8m-48< 0\Leftrightarrow-12< m< 4\)

\(\left(2\right)\Leftrightarrow-6\left(x^2-x+1\right)< 2x^2+mx-4\)

\(\Leftrightarrow8x^2+\left(m-6\right)x+2>0\)

Yêu cầu bài toán thỏa mãn khi \(\Delta=m^2-12m-28< 0\Leftrightarrow-2< x< 14\)

Vậy \(m\in\left(-2;4\right)\)

Đúng(3)

HP

Hồng Phúc

5 tháng 3 2021

2.

a, Yêu cầu bài toán thỏa mãn khi phương trình \(\left(m-4\right)x^2+\left(1+m\right)x+2m-1>0\) có nghiệm đúng với mọi x

\(\Leftrightarrow\left\{{}\begin{matrix}m-4>0\\\Delta=m^2+2m+1-4\left(m-4\right)\left(2m-1\right)< 0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m>4\\\left[{}\begin{matrix}m< \dfrac{3}{7}\\m>5\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow m>5\)

Đúng(3)

AA

Adorable Angel

13 tháng 3 2021

Giải hệ bpt

1) \(-4\le\dfrac{x^2-2x-7}{x^2+1}\le1\)

2) \(\dfrac{1}{13}\le\dfrac{x^2-2x-2}{x^2-5x+7}\le1\)

3) \(-1< \dfrac{10x^2-3x-2}{-x^2+3x-2}< 1\)

#Toán lớp 10

2

HP

Hồng Phúc

15 tháng 3 2021

1.

\(-4\le\dfrac{x^2-2x-7}{x^2+1}\le1\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2-2x-7\le x^2+1\\-4x^2-4\le x^2-2x-7\end{matrix}\right.\) (Do \(x^2+1>0\))

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-4\\\left[{}\begin{matrix}x\ge1\\x\le-\dfrac{3}{5}\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x\ge1\\-4\le x\le-\dfrac{3}{5}\end{matrix}\right.\)

Đúng(0)

HP

Hồng Phúc

15 tháng 3 2021

2.

\(\dfrac{1}{13}\le\dfrac{x^2-2x-2}{x^2-5x+7}\le1\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2-5x+7\le13x^2-26x-26\\x^2-2x-2\le x^2-5x+7\end{matrix}\right.\) (Do \(x^2-5x+7>0\))

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge\dfrac{11}{4}\\x\le-1\end{matrix}\right.\\x\le3\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{11}{4}\le x\le3\\x\le-1\end{matrix}\right.\)

Đúng(0)

A

abcd

21 tháng 2 2021

Xác định tất cả các tham số m sao cho :\(-1\le\dfrac{x^2+5x+m}{2x^2-3x+2}< 7\) \(\forall x\in R\)

#Toán lớp 10

1

DH

Đậu Hũ Kho

21 tháng 2 2021

\(-1\le\dfrac{x^2+5x+m}{2x^2-3x+2}< 7\) ∀x ∈ R

ta thấy \(2x^2-3x+2\) (*)vô nghiệm => * luôn dương ( cx dấu vs a)

\(\left\{{}\begin{matrix}\dfrac{x^2+5x+m}{2x^2-3x+2}+1\ge0\\\dfrac{x^2+5x+m}{2x^2-3x+2}-7< 0\end{matrix}\right.\)

\(\left\{{}\begin{matrix}3x^{2^{ }}+2x+m+2\ge0\\-13x^2+26x+m-14< 0\end{matrix}\right.\)

\(\left\{{}\begin{matrix}\left[{}\begin{matrix}a>0\\\Delta\le0\end{matrix}\right.\\\left[{}\begin{matrix}a< 0\\\Delta< 0\end{matrix}\right.\end{matrix}\right.\)

.....

tới đây bạn tự thế số vào làm tiếp nhé

Đ\Á :[\(\dfrac{-5}{3}\);1)

Đúng(2)

QT

Quoc Tran Anh Le

Giáo viên

26 tháng 9 2023

Tìm giá trị của m để:

a) \(2{x^2} + 3x + m + 1 > 0\) với mọi \(x \in \mathbb{R}\);

b) \(m{x^2} + 5x - 3 \le 0\) với mọi \(x \in \mathbb{R}\)

#Toán lớp 10

1

HQ

Hà Quang Minh

Giáo viên

26 tháng 9 2023

a) Tam thức \(2{x^2} + 3x + m + 1\) có \(\Delta = {3^2} - 4.2.\left( {m + 1} \right) = 1 - 8m\)

Vì \(a = 2 > 0\) nên để \(2{x^2} + 3x + m + 1 > 0\) với mọi \(x \in \mathbb{R}\) khi và chỉ khi \(\Delta < 0 \Leftrightarrow 1 - 8m < 0 \Leftrightarrow m > \frac{1}{8}\)

Vậy khi \(m > \frac{1}{8}\) thì \(2{x^2} + 3x + m + 1 > 0\) với mọi \(x \in \mathbb{R}\)

b) Tam thức \(m{x^2} + 5x - 3\) có \(\Delta = {5^2} - 4.m.\left( { - 3} \right) = 25 + 12m\)

Đề \(m{x^2} + 5x - 3 \le 0\) với mọi \(x \in \mathbb{R}\) khi và chỉ khi \(m < 0\) và \(\Delta = 25 + 12m \le 0 \Leftrightarrow m \le - \frac{{25}}{{12}}\)

Vậy \(m{x^2} + 5x - 3 \le 0\) với mọi \(x \in \mathbb{R}\) khi \(m \le - \frac{{25}}{{12}}\)

Đúng(0)

KH

Kimian Hajan Ruventaren

6 tháng 2 2021

Tìm m để hệ bất phương trình vô nghiệma) \(\left\{{}\begin{matrix}3x+4x+9\\1-2x\le m-3x+1\end{matrix}\right.\)b) \(\left\{{}\begin{matrix}2x+7\ge8x+1\\m+5< 2x\end{matrix}\right.\)c) \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge x^2+7x+1\\2m\le8+5x\end{matrix}\right.\)d) \(\left\{{}\begin{matrix}3x+5\ge x-1\\\left(x+2\right)^2\le\left(x-1\right)^2+9\\mx+1>\left(m-2\right)x+m\end{matrix}\right.\)e) \(\left\{{}\begin{matrix}2\left(x-3\right) 5\left(x-4\right)\\mx+1\le...

Đọc tiếp