MT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
13 tháng 5 2019
Phương trình đã cho có nghiệm khi ∆ ' = 1 - m ≥ 0 ⇔ m ≤ 1 .
Theo định lí Vi-ét, ta có: x 1 + x 2 = - 2 x 1 x 2 = m .
Kết hợp với điều kiện của bài toán 3 x 1 + 2 x 2 = 1 ta có hệ phương trình:
x 1 + x 2 = - 2 3 x 1 + 2 x 2 = 1 ⇔ x 1 = 5 x 2 = - 7
Do đó,x1.x2 = - 35= m (thỏa mãn m ≤ 1 ).
Chọn D.
NA
1
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 3 2022
- Với \(m=0\) ko thỏa mãn
- Với \(m\ne0\)
\(\Rightarrow m\left(x^3-8\right)-x^2+2x=0\)
\(\Leftrightarrow m\left(x-2\right)\left(x^2+2x+4\right)-x\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(mx^2+\left(2m-1\right)x+4m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\mx^2+\left(2m-1\right)x+4m=0\left(1\right)\end{matrix}\right.\)
Pt có 3 nghiệm pb lớn hơn 1 khi (1) có 2 nghiệm pb khác 2 và lớn hơn 1
\(\Rightarrow\left\{{}\begin{matrix}\Delta=\left(2m-1\right)^2-16m^2>0\\f\left(2\right)=4m+2\left(2m-1\right)+4m\ne0\\\left(x_1-1\right)\left(x_2-1\right)>0\\\dfrac{x_1+x_2}{2}>1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-12m^2-4m+1>0\\m\ne\dfrac{1}{6}\\x_1x_2-\left(x_1+x_2\right)+1>0\\x_1+x_2>2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-12m^2-4m+1>0\\m\ne\dfrac{1}{6}\\4+\dfrac{2m-1}{m}+1>0\\-\dfrac{2m-1}{m}>2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{1}{2}< m< \dfrac{1}{6}\\m\ne\dfrac{1}{6}\\\left[{}\begin{matrix}m< 0\\m>\dfrac{1}{7}\end{matrix}\right.\\0< m< \dfrac{1}{4}\end{matrix}\right.\) \(\Leftrightarrow\dfrac{1}{7}< m< \dfrac{1}{6}\)
CM
6 tháng 11 2018
Điều kiện: -1 < x < 1.
Với điều kiện trên, phương trình đã cho tương đương: x = 5- 2m
Để phương trình đã cho có nghiệm thì: -1 < 5- 2m < 1
⇔ - 6 < - 2 m < - 4 ⇔ 3 > m > 2 .
CM
18 tháng 6 2018
Ta có: m - 1 x + 6 ≥ 0 ; x + 2 ≥ 0 . Do đó,
m - 1 x + 6 + x + 2 = 0 ⇔ m - 1 x + 6 = 0 x + 2 = 0 ⇔ m - 1 . - 2 + 6 = 0 x = - 2 ⇔ - 2 m + 2 + 6 = 0 x = - 2 ⇔ m = 4 x = - 2
Chọn A.
CM
16 tháng 7 2018
Để phương trình đã cho có 2 nghiệm trái dấu thì:
ac = -m - 6 < 0 hay m > - 6
HP
4 tháng 5 2021
b, \(d\left(I;\Delta\right)=R\Leftrightarrow\dfrac{\left|-2+6+m\right|}{\sqrt{13}}=\sqrt{13}\)
\(\Rightarrow\left[{}\begin{matrix}m=9\\m=-17\end{matrix}\right.\)
HP
4 tháng 5 2021
c, Dễ tìm được tọa độ A, B: \(\left\{{}\begin{matrix}A=\left(-3,-1\right)\\B=\left(2,0\right)\end{matrix}\right.\)
Phương trình tiếp tuyến tại A có dạng: \(\Delta_1:ax+by+3a+b=0\left(a^2+b^2\ne0\right)\)
Ta có: \(d\left(I,\Delta_1\right)=\dfrac{\left|-a+2b+3a+b\right|}{\sqrt{a^2+b^2}}=\sqrt{13}\)
\(\Leftrightarrow\left(2a+3b\right)^2=13a^2+13b^2\)
\(\Leftrightarrow4a^2+9b^2+12ab=13a^2+13b^2\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow9a^2+4b^2-12ab=0\)
\(\Leftrightarrow3a=2b\)
\(\Rightarrow\Delta_1:2x+3y+9=0\)
Tương tự tiếp tuyến tại B: \(\Delta_2:3x-2y-6=0\)
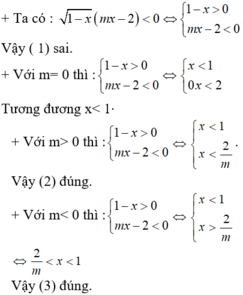
\(m\in\left[-4;5\right]\)