Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Ta có y ' = − m + 1 x − 1 2
hàm số đồng biến trên từng khoảng xác định của nó ⇔ y ' > 0 ⇔ − m − 1 > 0 ⇔ m < − 1

Đáp án D
Ta có y ' = 1 − m x + 1 2
Để hàm số đồng biến trên từng khoảng xác định
⇔
y
'
>
0
,
∀
x
∈
D
=
ℝ
\
±
1
⇒
1
−
m
>
0
⇔
m
<
1

Tập xác định: D = R ∖ { 1 }
· y ' = m x 2 + 2 m x + 1 x + 1 2
· Hàm số luôn đồng biến trên từng khoảng xác định của nó khi và chỉ khi y ' > 0; ∀ x ≠ 1
· Xét m = 0, ta có y ' = 1 x + 1 2 > 0 ; ∀ x ≠ 1 (tm).
· Xét m ≠ 0 .Yêu cầu bài toán
⇔ ∆ ' = m 2 - m ≤ 0 m > 0 ⇔ 0 ≤ m ≤ 1 m > 0 ⇔ 0 < m ≤ 1
Kết luận: 0 ≤ m ≤ 1
Đáp án B

Đáp án C
Ta có y ' = 4 − m 2 x − 1 2 hàm số đồng biến trên tập xác định của nó
⇔ 4 − m 2 > 0 ⇔ − 2 < m < 2 do m nguyên ⇒ m = 0, m = ± 1
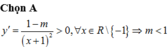
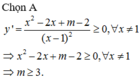


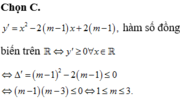
Đáp án là A.
TXĐ: D = ℝ \ − 1 .
Ta có: y ' = 1 + m x + 1 2
Hàm số đồng biến trên 2 khoảng xác định ⇔ 1 + m > 0 ⇔ m > − 1