MV
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
Z2
1
24 tháng 12 2021
Hoàng độ giao điểm của y= x^2 và y = 2x + 3 là nghiệm phương trình:
x^2 = 2x + 3 <=> x^2 -2x - 3 = 0 <=> x = 3 hoặc x = -1
Vì giao điểm của 3 đồ thị là điểm thuộc góc phần tư thứ 2 => hoành độ giao điệm x < 0
=> x = 3 loại
x = -1 thỏa mãn
Với x = -1 => y = 1
khi đó: 1 = ( 2m - 3) ( -1) + m - 5
<=> 1 = -2m + 3 + m - 5
<=> m = -3
9 tháng 7 2020
Hoàng độ giao điểm của y= x^2 và y = 2x + 3 là nghiệm phương trình:
x^2 = 2x + 3 <=> x^2 -2x - 3 = 0 <=> x = 3 hoặc x = -1
Vì giao điểm của 3 đồ thị là điểm thuộc góc phần tư thứ 2 => hoành độ giao điệm x < 0
=> x = 3 loại
x = -1 thỏa mãn
Với x = -1 => y = 1
khi đó: 1 = ( 2m - 3) ( -1) + m - 5
<=> 1 = -2m + 3 + m - 5
<=> m = -3
TH
2
3 tháng 12 2023
Phương trình hoành độ giao điểm là:
\(\left(m-1\right)x+2m+3=2x+1\)
=>\(\left(m-1\right)x-2x=1-2m-3\)
=>\(x\left(m-3\right)=-2m-2\)
=>\(x=\dfrac{-2m-2}{m-3}\)
\(y=2x+1=\dfrac{2\cdot\left(-2m-2\right)}{m-3}+1=\dfrac{-4m-4+m-3}{m-3}=\dfrac{-3m-7}{m-3}\)
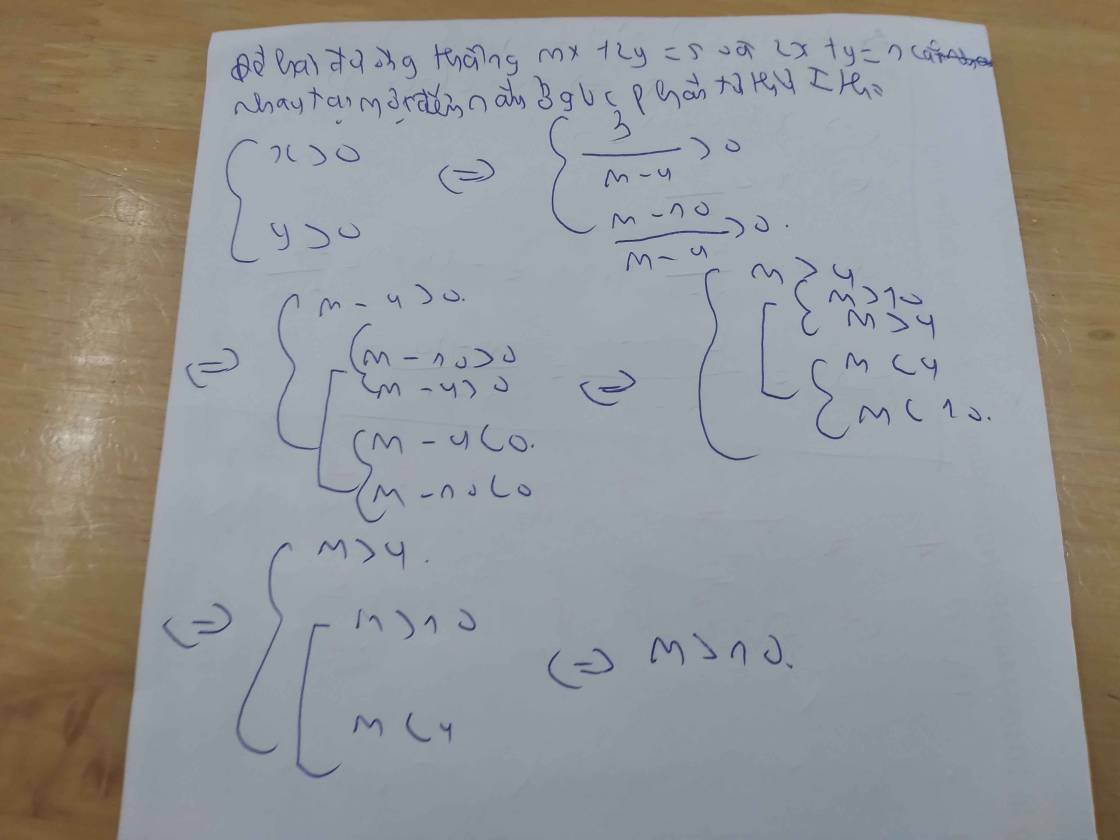
Để (d) cắt đường thẳng y=2x+1 tại một điểm thuộc góc phần tư thứ nhất thì
\(\left\{{}\begin{matrix}m-1\ne2\\\dfrac{-2m-2}{m-3}< 0\\\dfrac{-3m-7}{m-3}>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne2\left(5\right)\\\dfrac{m+1}{m-3}>0\left(1\right)\\\dfrac{3m+7}{m-3}< 0\left(2\right)\end{matrix}\right.\)
(1); \(\dfrac{m+1}{m-3}>0\)
TH1: \(\left\{{}\begin{matrix}m+1>0\\m-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-1\\m>3\end{matrix}\right.\)
=>m>3
TH2: \(\left\{{}\begin{matrix}m+1< 0\\m-3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m< -1\\m< 3\end{matrix}\right.\)
=>m<-1
Vậy: \(m\in\left(3;+\infty\right)\cup\left(-\infty;-1\right)\)(3)
(2): \(\dfrac{3m+7}{m-3}< 0\)
TH1: \(\left\{{}\begin{matrix}3m+7>0\\m-3< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>-\dfrac{7}{3}\\m< 3\end{matrix}\right.\)
=>\(\dfrac{-7}{3}< m< 3\)
TH2: \(\left\{{}\begin{matrix}3m+7< 0\\m-3>0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m>3\\m< -\dfrac{7}{3}\end{matrix}\right.\)
=>Loại
Vậy: \(-\dfrac{7}{3}< m< 3\)(4)
Từ (3),(4),(5) suy ra \(\left\{{}\begin{matrix}m\ne2\\-\dfrac{7}{3}< m< 3\\m\in\left(3;+\infty\right)\cup\left(-\infty;-1\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\ne2\\m\in\left(-\dfrac{7}{3};-1\right)\end{matrix}\right.\)
=>\(m\in\left(-\dfrac{7}{3};-1\right)\)
MC
0
31 tháng 5 2021
Xét pt hoành độ giao điểm:
(m - 3)x + 2m - 4 = -x + 5
\(\Leftrightarrow\) mx - 3x + 2m - 4 = -x + 5
\(\Leftrightarrow\) m(x + 2) = 2x + 9
\(\Leftrightarrow\) m = \(\dfrac{2x+9}{x+2}\)
Vì 2 đường thẳng cắt nhau tại 1 điểm nằm trong góc phần tư thứ 1
\(\Rightarrow\) x > 0
\(\Leftrightarrow\) 2x + 9 > 9; x + 2 > 2
\(\Rightarrow\) \(\dfrac{2x+9}{x+2}>\dfrac{9}{2}\)
\(\Leftrightarrow\) m \(>\dfrac{9}{2}\)
Vậy \(m>\dfrac{9}{2}\)
Chúc bn học tốt!
16 tháng 4 2021
Xét phương trình hoành độ giao điểm 2 đường thẳng trên ta có:
$2x-m-3=m-4$
$⇒x=\dfrac{2m-1}{2}$
Nên điểm đó có tọa độ $M(\dfrac{2m-1}{2};m-4)$
suy ra điểm đó nằm trong góc phần tư thứ (VI) của mặt phẳng
\(\left\{{}\begin{matrix}\dfrac{2m-1}{2}>0\\m-4< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{1}{2}\\m< 4\end{matrix}\right.\)
Mà $m∈Z$ nên \(m\in\left\{1;2;3\right\}\)
$m=1⇒M(\dfrac{1}{2};-3)$
$m=2⇒M(\dfrac{3}{2};-2)$
$m=3⇒M(\dfrac{5}{2};-1)$
Vậy \(m\in\left\{1;2;3\right\}\)thỏa mãn đề
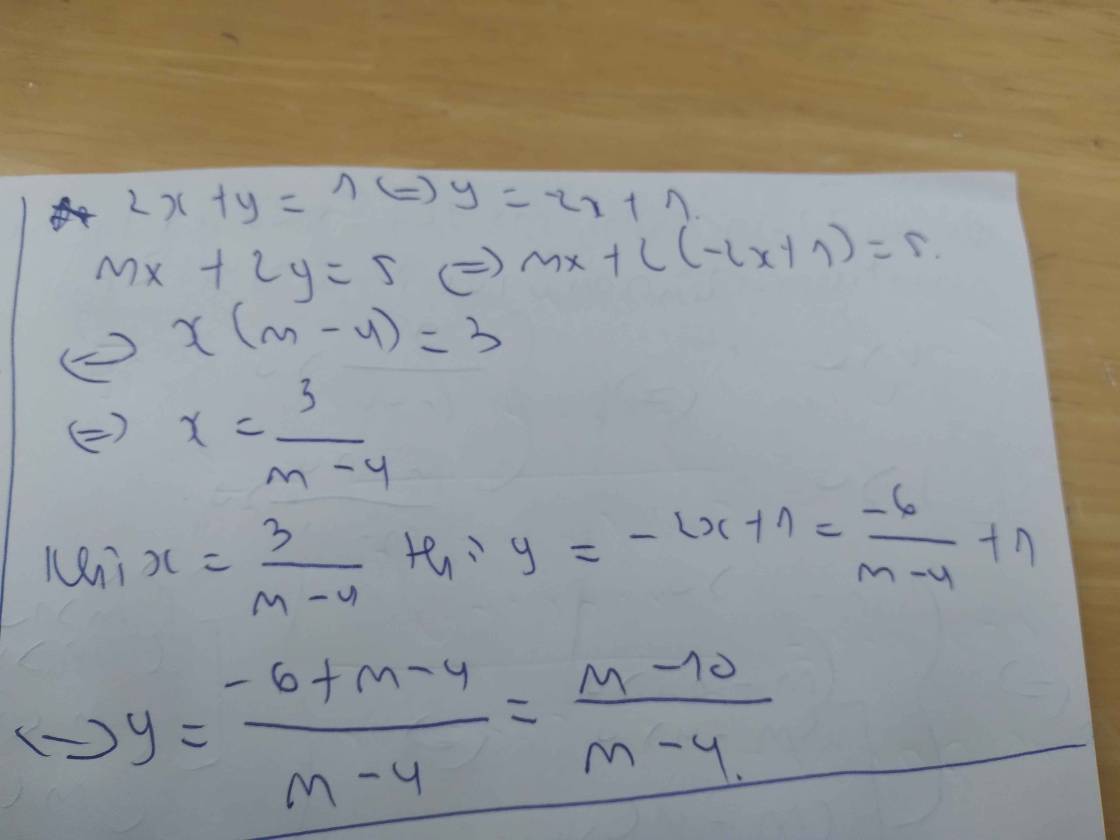
Phương trình hoành độ giao điểm:
\(x+3=2x+m-1\Rightarrow x=4-m\)
\(\Rightarrow y=x+3=7-m\)
Giao điểm nằm ở góc phần tư thứ 2 khi: \(\left\{{}\begin{matrix}x< 0\\y>0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}4-m< 0\\7-m>0\end{matrix}\right.\) \(\Rightarrow4< m< 7\)