Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm của (P) và d là x 2 - m x - 1 = 0
Ta có ∆ = m 2 + 4 > 0 ∀ m . Suy ra phương trình luôn có 2 nghiệm phân biệt x 1 ; x 2
Giả sử x 1 < x 2 . Khi đó:
S = ∫ x 1 x 2 m x + 2 - x 2 - 1 d x = ∫ x 1 x 2 m x + 1 - x 2 d x = m 2 + 4 m 2 6 + 2 3 ≥ 4 3
Vậy m i n S = 4 3 ⇔ m = 0
Đáp án D





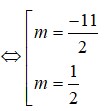
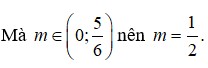

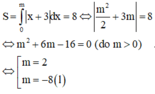

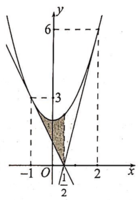
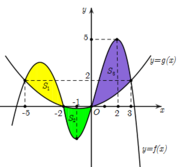
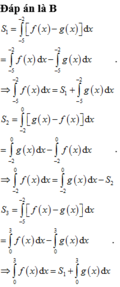

Phương trình hoành độ giao điểm của (P) và d là
- x 2 + 2 x = m x ⇔ x 2 - 2 - m x = 0 ⇔ x = 0 x = 2 - m > 0
Khi đó
S = ∫ 0 2 - m - x 2 + 2 x - m x d x = ∫ 0 2 - m - x 2 + 2 x - m x = - x 3 3 + x 2 - m x 2 2 0 2 - m = - m 3 + 6 m 2 - 12 m + 8 = 27
Do đó m 3 - 6 m 2 + 12 m + 9 = 0
Giải phương trình này, ta tìm được m = -1 là giá trị thỏa yêu cầu bài toán.
Đáp án A