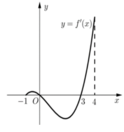
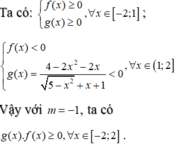Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
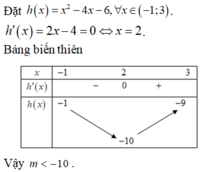
Đặt ![]()
Yều cẩu bào toán trở thành: Tìm m để bất phương trình ![]() nghiệm đúng với mọi
nghiệm đúng với mọi ![]()
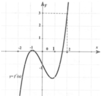
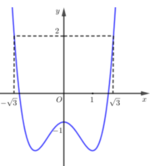
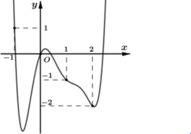
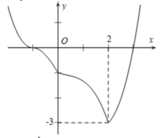
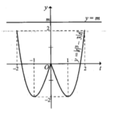
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kết quả thỏa mãn yêu cầu bài toán là ![]()

Đáp án B
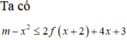
![]()
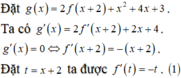
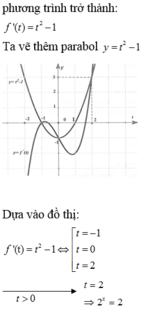
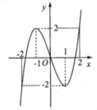
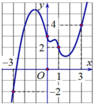
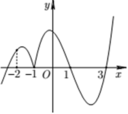
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
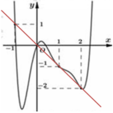
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có




\(\Leftrightarrow2^{2x}-1+m.2^x+m\le0\\ \Leftrightarrow\left(2^x-1\right)\left(2^x+1\right)+m\left(2^x+1\right)\le0\\ \Leftrightarrow\left(2^x+1\right)\left(2^x-1+m\right)\le0\)
Vì \(2^x+1>0\forall x\) nên ta có
\(2^x-1+m\le0\Leftrightarrow2^x\le1-m\)
Vẽ đồ thị hàm số \(f\left(x\right)=2^x\),
ta thấy bất phương trình có nghiệm khi và chỉ khi đường thẳng y=1-m nằm trên trục Ox
\(\Rightarrow1-m>0\Leftrightarrow m< 1\) (không có dấu "=")