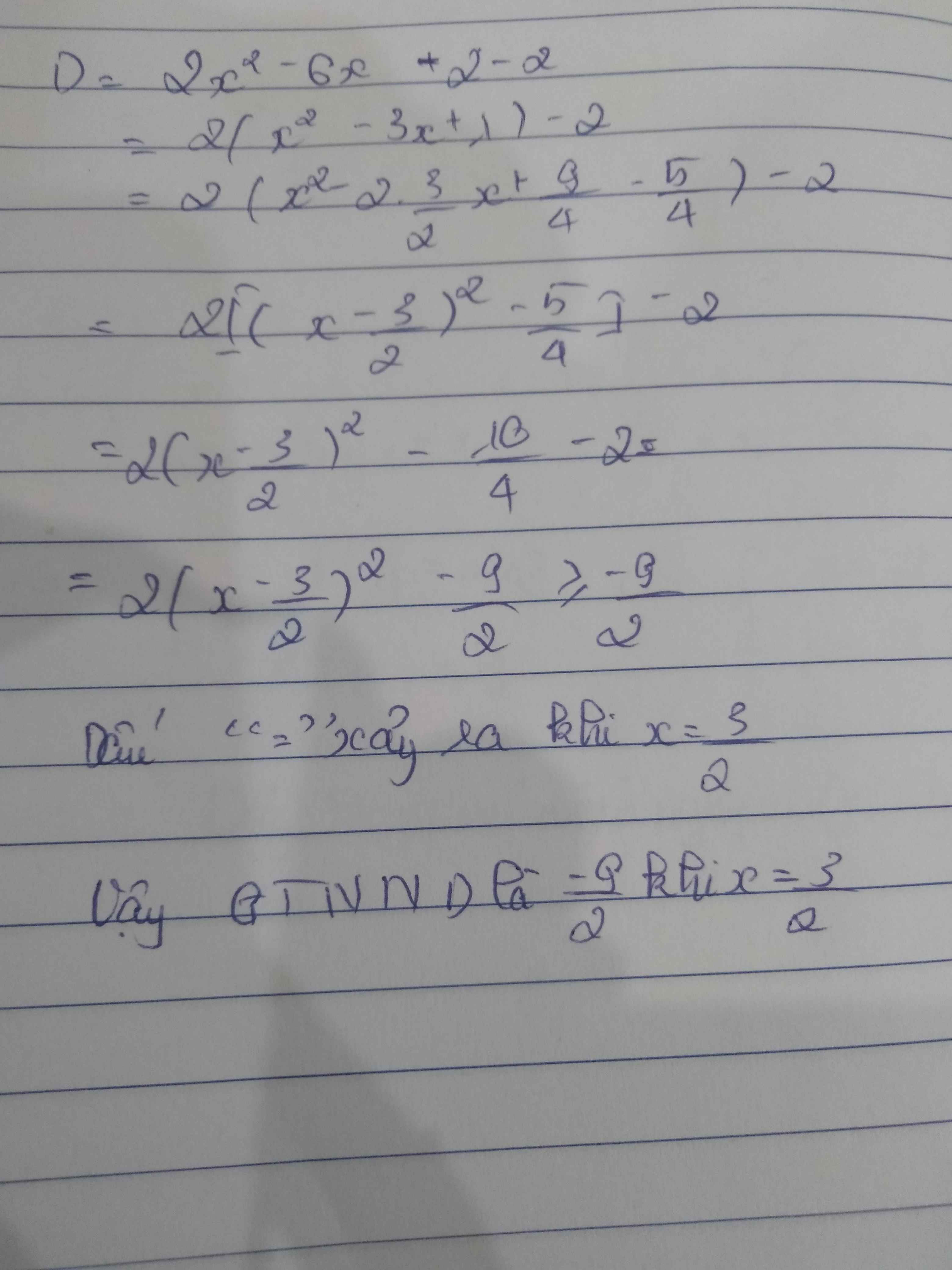Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





D= 2x2 - 6x
= 2(x2 - 3x +\(\dfrac{9}{4}\)) - \(\dfrac{9}{2}\)
= 2[x2 - 2.x.\(\dfrac{3}{2}\) + (\(\dfrac{3}{2}\))2 ] - \(\dfrac{9}{2}\)
= 2 (x - \(\dfrac{3}{2}\))2 - \(\dfrac{9}{2}\)
Ta có:
2(x - \(\dfrac{3}{2}\))2 ≥ 0 ⇒ 2 (x - \(\dfrac{3}{2}\))2 - \(\dfrac{9}{2}\) ≥ -\(\dfrac{9}{2}\)
Hay D≥ -\(\dfrac{9}{2}\)
Dấu = xảy ra ⇔ (x - \(\dfrac{3}{2}\)) = 0 ⇔ x = \(^{\dfrac{3}{2}}\)
Vậy MinD = - \(\dfrac{9}{2}\) ⇔ x = \(\dfrac{3}{2}\)


Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{2x+1}{5}=\frac{3y-2}{7}=\frac{2x+3y-1}{6x}=\frac{2x+1+3y-2-2x-3y+1}{5+7-6x}=\frac{0}{12-6x}=0\)
\(\left[\begin{array}{nghiempt}2x+1=0\\3y-2=0\end{array}\right.\)
\(\left[\begin{array}{nghiempt}2x=-1\\3y=2\end{array}\right.\)
\(\left[\begin{array}{nghiempt}x=-\frac{1}{2}\\y=\frac{2}{3}\end{array}\right.\)
Giải:
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{2x+1}{5}=\frac{3y-2}{7}=\frac{2x+3y+1-2}{5+7}=\frac{2x+3y-1}{12}=\frac{2x+3y-1}{6x}\)
+) Xét \(2x+3y-1=0\Rightarrow2x+1=0=3y-2=0\)
\(\Rightarrow x=\frac{-1}{2},y=\frac{2}{3}\)
+) Xét \(2x+3y-1\ne0\)
\(\Rightarrow6x=12\)
\(\Rightarrow x=2\)
Ta có: \(2x+1=3y-2\)
\(\Rightarrow2.2+1=3y-2\)
\(\Rightarrow5=3y-2\)
\(\Rightarrow3y=7\)
\(\Rightarrow y=\frac{7}{3}\)
Vậy bộ số \(\left(x,y\right)\) là \(\left(\frac{-1}{2},\frac{2}{3}\right);\left(2,\frac{7}{3}\right)\)

A+B=0
=> (x2-6x-7)+(-x2+2x+3)=0
=> x2-6x-7-x2+2x+3=0
=> (x2-x2)+(-6x+2x)+(-7+3)=0
=> -4x-4=0
=> -4x=4
=> x=-1
Ta có A+B=0
=> (x2-6x-7)+(-x2+2x)=0
=> x2-6x-7-x2+2x=0
=> (x2-x2)-(6x-2x)-7=0
=> -4x-7=0
=> -4x=7
=> x=7:(-4)
=> x= -1,75