K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DN
0
TV
1
27 tháng 2 2018
A = (x^2+x).(x^2+x-4)
= (x^2+x-2+2).(x^2+x-2-2)
= (x^2+x-2)^2 - 2^2
= (x^2+x-2)^2 - 4 >= -4
Dấu "=" xảy ra <=> x^2+x-2 = 0 <=> x=1 hoặc x=-2
Vậy GTNN của A = -4 <=> x=1 hoặc x=-2
Tk mk nha
13 tháng 9 2021
\(6,\\ a,\\ 1,A=x^2+3x+7=\left(x+\dfrac{3}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}\)
Dấu \("="\Leftrightarrow x=-\dfrac{3}{2}\)
\(2,B=\left(x-2\right)\left(x-5\right)\left(x^2-7x+10\right)=\left(x-2\right)^2\left(x-5\right)^2\ge0\)
Dấu \("="\Leftrightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)
\(b,\\ 1,A=11-10x-x^2=-\left(x+5\right)^2+36\le36\)
Dấu \("="\Leftrightarrow x=-5\)
DN
1
DD
Đoàn Đức Hà
Giáo viên
26 tháng 6 2021
\(A=\frac{5x^2+4x-1}{x^2}=\frac{9x^2-\left(4x^2-4x+1\right)}{x^2}=9-\frac{\left(2x-1\right)^2}{x^2}\le9\)
Dấu \(=\)khi \(2x-1=0\Leftrightarrow x=\frac{1}{2}\).
\(B=\frac{x^2}{x^2+x+1}=\frac{3x^2}{3x^2+3x+3}=\frac{4x^2+4x+4-\left(x^2+4x+4\right)}{3x^2+3x+3}=\frac{4}{3}-\frac{\left(x+2\right)^2}{3\left(x^2+x+1\right)}\le\frac{4}{3}\)
Dấu \(=\)khi \(x+2=0\Leftrightarrow x=-2\).
ND
1
LM
3 tháng 9 2016
a/ M = -x2 - 2x + 7 = -(x2 + 2x - 7) = -(x2 + 2 . x + 1 - 8) = -[ (x + 1)2 - 8] = -(x + 1)2 + 8 \(\le\)8
Đẳng thức xảy ra khi: -(x + 1)2 = 0 => x = -1
Vậy giá trị lớn nhất của M là 8 khi x = -1
b/ N = -x2 + 4x + 5 = -(x2 - 4x - 5) = -(x2 - 2 . 2x + 22 - 9) = -[ (x - 2)2 - 9] = -(x - 2)2 + 9 \(\le\)9
Đẳng thức xảy ra khi: -(x - 2)2 = 0 => x = 2
Vậy giá trị lớn nhất của N là 9 khi x = 2
NK
1
DD
Đoàn Đức Hà
Giáo viên
6 tháng 11 2021
a) \(A=6x-x^2-11=-\left(x^2-6x+9\right)-2=-\left(x-3\right)^2-2\le-2\)
Dấu \(=\)khi \(x-3=0\Leftrightarrow x=3\).
b) \(B=x^2-5x-2=x^2-2.\frac{5}{2}x+\left(\frac{5}{2}\right)^2-\frac{33}{4}=\left(x-\frac{5}{2}\right)^2-\frac{33}{4}\ge-\frac{33}{44}\)
Dấu \(=\)khi \(x-\frac{5}{2}=0\Leftrightarrow x=\frac{5}{2}\).
2 tháng 8 2016
E XIN LỖI CHỊ , NHƯNG E MỚI HỌC LỚP 6
THÌ GIÚP CHỊ KIỂU GÌ Ạ ???
THÔI THÌ CHÚC CHỊ SẼ CHỌN ĐC CÂU TRẢ LỜI ƯNG Ý VỚI MK NHÉ ! MỌI NGƯỜI GIÚP CHỊ NHA !
2 tháng 8 2016
\(x-x^2+1\)
\(=-\left(x^2-x-1\right)\)
\(=-\left(x^2-2.x.\frac{1}{2}+\frac{1}{4}-\frac{5}{4}\right)\)
\(=-\left(\left(x-\frac{1}{2}\right)^2-\frac{5}{4}\right)\)
\(=\frac{5}{4}-\left(x-\frac{1}{2}\right)^2\le\frac{5}{4}\)
Max\(=\frac{5}{4}\Leftrightarrow x-\frac{1}{2}=0\Rightarrow x=\frac{1}{2}\)
NT
Tìm GTLN, GTNN của biểu thức sau
\(1,A=\left(x-1\right)^2-10\)
\(2,B=-|x-1|-2\left(2y-1\right)^2+100\)
2
12 tháng 5 2022
1: \(A=\left(x-1\right)^2-10\ge-10\)
Dấu '=' xảy ra khi x=1
2: \(B=-\left|x-1\right|-2\cdot\left(2y-1\right)^2+100\le100\)
Dấu '=' xảy ra khi x=1 và y=1/2
12 tháng 5 2022
`(x-1)^2 >=0 => (x-1)^2 - 10 >= -10`
Dấu bằng xảy ra khi `x = 1`.
Vì `-|x-1| <=0, -2(2y-1)^2 <= 0`
`=> -|x-1| - 2(2y-1)^2 + 100 <= 100`
Dấu bằng xảy ra `<=> x = 1, y = 1/2`.
G
1
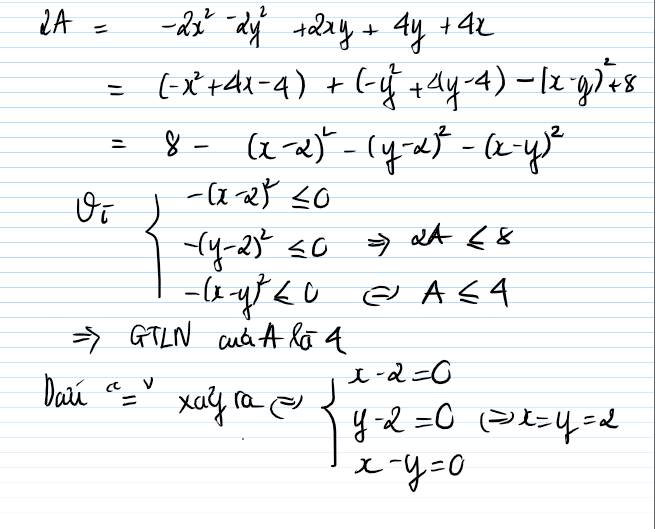
ta có:
x2 ≥0
=>- x2≤0
=> -x2+x≤0
A=-x2+x=0
=> A=x(1-x)=0
=> _x=0
|_x=1
=> max của A là 0 tại x =1 hoặc x=0
đây phải là tìm GTLN chứ