
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

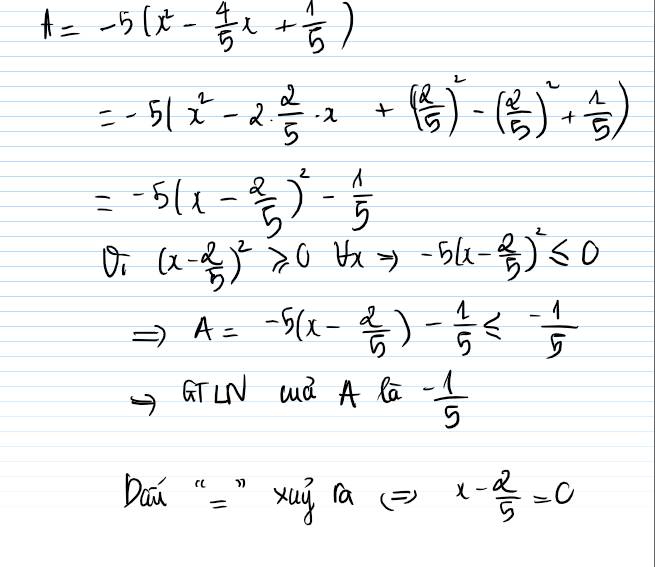

Ta có:
\(B=-5x^2-4x+1\)
\(=\left(4x^2-4x+1\right)-9x^2\)
\(=\left(2x-1\right)^2-\left(3x\right)^2\)
\(=\left(2x-1+3x\right)\left(2x-1-3x\right)\)
\(=-\left(x+1\right)\left(5x-1\right)\)
\(B=-5x^2-4x+1\)
\(B=-5\left(x^2+\frac{4}{5}x-\frac{1}{5}\right)\)
\(B=-5\left[x^2+2.x.\frac{2}{5}+\left(\frac{2}{5}\right)^2-\frac{9}{25}\right]\)
\(B=-5\left(x+\frac{2}{5}\right)^2+5.\frac{9}{25}\)
\(B=-5\left(x+\frac{2}{5}\right)^2+\frac{9}{5}\)
Ta có: \(\left(x+\frac{2}{5}\right)^2\ge0\forall x\)
\(\Rightarrow-5.\left(x+\frac{2}{5}\right)^2\le0\forall x\)
\(\Rightarrow-5.\left(x+\frac{2}{5}\right)^2+\frac{9}{5}\le\frac{9}{5}\forall x\)
\(B=\frac{9}{5}\Leftrightarrow-5.\left(x+\frac{2}{5}\right)^2=0\Leftrightarrow x+\frac{2}{5}=0\Leftrightarrow x=-\frac{2}{5}\)
Vậy \(B_{max}=\frac{9}{5}\Leftrightarrow x=-\frac{2}{5}\)
Tham khảo nhé~

\(A=\frac{5x^2+4x-1}{x^2}=\frac{9x^2-\left(4x^2-4x+1\right)}{x^2}=9-\frac{\left(2x-1\right)^2}{x^2}\le9\)
Dấu \(=\)khi \(2x-1=0\Leftrightarrow x=\frac{1}{2}\).
\(B=\frac{x^2}{x^2+x+1}=\frac{3x^2}{3x^2+3x+3}=\frac{4x^2+4x+4-\left(x^2+4x+4\right)}{3x^2+3x+3}=\frac{4}{3}-\frac{\left(x+2\right)^2}{3\left(x^2+x+1\right)}\le\frac{4}{3}\)
Dấu \(=\)khi \(x+2=0\Leftrightarrow x=-2\).

Bài 2:
a: Ta có: \(x^2+4x+7\)
\(=x^2+4x+4+3\)
\(=\left(x+2\right)^2+3\ge3\forall x\)
Dấu '=' xảy ra khi x=-2

Con xin lỗi con ghi sai đề ạ . Có thể giải lại giúp con không ạ


A = - 4\(x\)2 + 5\(x\) - 3
A = -( 4\(x^2\) - 5\(x\) + \(\dfrac{25}{16}\)) - \(\dfrac{23}{16}\)
A = -( 2\(x\) - \(\dfrac{5}{4}\))2 - \(\dfrac{23}{16}\)
Vì ( 2\(x\) - \(\dfrac{5}{4}\))2 ≥ 0; ⇒ - ( 2\(x\) - \(\dfrac{5}{4}\))2 ≤ 0 ⇒ -( 2 \(x\) - \(\dfrac{5}{4}\))2 - \(\dfrac{23}{16}\) ≤ - \(\dfrac{23}{16}\)
A(max) = - \(\dfrac{23}{16}\) ⇔ 2\(x\) - \(\dfrac{5}{4}\) = 0 ⇔ \(x\) = \(\dfrac{5}{4}\): 2 = \(\dfrac{5}{8}\)
Kết luận giá trị lớn nhất của biểu thức là - \(\dfrac{23}{16}\) xáy ra khi \(x\) = \(\dfrac{5}{8}\)

\(A=\frac{2}{-5x^2+3x+2}=\frac{2}{\left(-5x^2+3x-\frac{9}{20}\right)+\frac{49}{20}}\)
\(A=\frac{2}{-5\left(x^2-\frac{3}{5}+\frac{9}{100}\right)+\frac{49}{20}}=\frac{2}{-5\left(x-\frac{3}{10}\right)^2+\frac{49}{20}}\ge\frac{2}{\frac{49}{20}}=\frac{40}{49}\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(-5\left(x-\frac{3}{10}\right)^2=0\)\(\Leftrightarrow\)\(x=\frac{3}{10}\)
Vậy GTNN của \(A\) là \(\frac{40}{49}\) khi \(x=\frac{3}{10}\)
\(B=\frac{5}{5x^2+4x+1}=\frac{5}{\left(5x^2+4x+\frac{4}{5}\right)+\frac{1}{5}}\)
\(B=\frac{5}{5\left(x^2+\frac{4}{5}x+\frac{4}{25}\right)+\frac{1}{5}}=\frac{5}{5\left(x+\frac{2}{5}\right)^2+\frac{1}{5}}\le\frac{5}{\frac{1}{5}}=25\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(5\left(x+\frac{2}{5}\right)^2=0\)\(\Leftrightarrow\)\(x=\frac{-2}{5}\)
Vậy GTLN của \(B\) là \(25\) khi \(x=\frac{-2}{5}\)
Chúc bạn học tốt ~
a) Ta có: A bé nhất khi \(-5x^2+3x+2\) lớn nhất
Ta có: \(-5x^2+3x+2=\left(-5x^2+3x-\frac{9}{20}\right)+\frac{49}{20}\)
\(=-5\left(x^2-2.\frac{3}{10}+\frac{9}{100}\right)=-5\left(x-\frac{3}{10}\right)^2+\frac{49}{20}\le\frac{49}{20}\)
Do đó \(A=\frac{2}{-5\left(x-\frac{3}{10}\right)^2+\frac{49}{20}}\le\frac{40}{49}\)
Dấu "=" xảy ra \(\Leftrightarrow-5\left(x-\frac{3}{10}\right)^2=0\Leftrightarrow x=\frac{3}{10}\)
Vậy \(A_{max}=\frac{40}{49}\Leftrightarrow x=\frac{3}{10}\)
b) Để B lớn nhất thì \(5x^2+4x+1\) bé nhất.Ta có:
\(5x^2+4x+1=\left(5x^2+4x\right)+1\)
\(=5\left(x^2+\frac{4}{5}x\right)+1=5\left(x^2+2.\frac{4}{10}+\frac{4}{25}\right)+\frac{1}{5}\)
\(=5\left(x+\frac{2}{5}\right)^2+\frac{1}{5}\ge\frac{1}{5}\)
Do đó \(B=\frac{5}{5\left(x+\frac{2}{5}\right)^2}\le\frac{5}{\frac{1}{5}}=25\)
Dấu "=" xảy ra \(\Leftrightarrow5\left(x+\frac{2}{5}\right)^2=0\Leftrightarrow x=-\frac{2}{5}\)
Vậy \(B_{max}=25\Leftrightarrow x=-\frac{2}{5}\)


\(A=\dfrac{4\left(x^2-4x+4\right)+\left(x^2-8x+16\right)}{x^2-4x+4}=4+\left(\dfrac{x-4}{x-2}\right)^2\ge4\)
\(A_{min}=4\) khi \(x=4\) (A max ko tồn tại)
\(B=\dfrac{6\left(x^2+2x+1\right)+\left(4x^2+12x+9\right)}{x^2+2x+1}=6+\left(\dfrac{2x+3}{x+1}\right)^2\ge6\)
\(B_{min}=6\) khi \(x=-\dfrac{3}{2}\)
B max ko tồn tại