Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
L = lim x → 1 1 − x 2 − x − 1 = lim x → 1 1 − x 2 − x + 1 1 − x = lim x → 1 2 − x + 1 = 2

\(\lim\limits_{x\rightarrow1}\frac{x^4+x^3-2}{x^5-x^2}=\lim\limits_{x\rightarrow1}\frac{x^4-1+x^3-1}{x^2\left(x^3-1\right)}\)
\(=\lim\limits_{x\rightarrow1}\frac{\left(x^2-1\right)\left(x^2+1\right)+\left(x-1\right)\left(x^2+x+1\right)}{x^2\left(x-1\right)\left(x^2+x+1\right)}\)\(=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left[\left(x+1\right)\left(x^2+1\right)+\left(x^2+x+1\right)\right]}{x^2\left(x-1\right)\left(x^2+x+1\right)}\)\(=\lim\limits_{x\rightarrow1}\frac{\left[\left(x+1\right)\left(x^2+1\right)+\left(x^2+x+1\right)\right]}{x^2\left(x^2+x+1\right)}\)=\(\frac{7}{3}\)
=lim x^2(x^2+x) - 2 \ x^2(x^3-1)=lim(x^2+x)\(x^3-1)=lim 2\-2=-1

Phương pháp:
Phân tích đa thức thành nhân tử. Rút gọn khử dạng 0 0
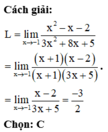

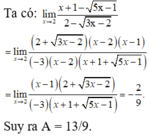
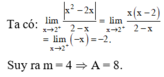
Đáp án A
Ta có: L = lim x → + ∞ x + 1 − x 2 − x + 2 = lim x → + ∞ 3 x − 1 x + 1 + x 2 − x + 2 = 3 2 .