GS
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
3 tháng 9 2021
\(\left|x-\dfrac{2}{3}\right|-4\ge-4\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{2}{3}\)
GB
1
KV
20 tháng 3 2023
A = 5x² + 6
Do x² ≥ 0
⇒ 5x² ≥ 0
⇒ 5x² + 6 ≥ 6
Vậy giá trị nhỏ nhất của A là 6 khi x = 0
--------------------
B = 4(2x - 4)² + 2023
Do (2x - 4)² ≥ 0
⇒ 4(2x - 4)² ≥ 0
⇒ 4(2x - 4)² + 2023 ≥ 2023
Vậy giá trị nhỏ nhất của B là 2023 khi x = 2
TA
23 tháng 7 2021
1) `(x-3)^4 >=0`
`2.(x-3)^4>=0`
`2.(x-3)^4-11 >=-11`
`=> A_(min)=-11 <=> x-3=0<=>x=3`
2) `|5-x|>=0`
`-|5-x|<=0`
`-3-|5-x|<=-3`
`=> B_(max)=-3 <=>x=5`.
24 tháng 7 2021
Bài 1:
Ta có: \(\left(x-3\right)^4\ge0\forall x\)
\(\Leftrightarrow2\left(x-3\right)^4\ge0\forall x\)
\(\Leftrightarrow2\left(x-3\right)^4-11\ge-11\forall x\)
Dấu '=' xảy ra khi x=3
DN
1
AH
Akai Haruma
Giáo viên
20 tháng 6 2023
$A=(x-4)^2+1$
Ta thấy $(x-4)^2\geq 0$ với mọi $x$
$\Rightarroe A=(x-4)^2+1\geq 0+1=1$
Vậy GTNN của $A$ là $1$. Giá trị này đạt tại $x-4=0\Leftrightarrow x=4$
-------------------
$B=|3x-2|-5$
Vì $|3x-2|\geq 0$ với mọi $x$
$\Rightarrow B=|3x-2|-5\geq 0-5=-5$
Vậy $B_{\min}=-5$. Giá trị này đạt tại $3x-2=0\Leftrightarrow x=\frac{2}{3}$
AH
Akai Haruma
Giáo viên
20 tháng 6 2023
$C=5-(2x-1)^4$
Vì $(2x-1)^4\geq 0$ với mọi $x$
$\Rightarrow C=5-(2x-1)^4\leq 5-0=5$
Vậy $C_{\max}=5$. Giá trị này đạt tại $2x-1=0\Leftrightarrow x=\frac{1}{2}$
----------------
$D=-3(x-3)^2-(y-1)^2-2021$
Vì $(x-3)^2\geq 0, (y-1)^2\geq 0$ với mọi $x,y$
$\Rightarrow D=-3(x-3)^2-(y-1)^2-2021\leq -3.0-0-2021=-2021$
Vậy $D_{\max}=-2021$. Giá trị này đạt tại $x-3=y-1=0$
$\Leftrightarrow x=3; y=1$
18 tháng 3 2021
a) Ta có: \(\left(x-2\right)^2\ge0\forall x\)
nên Dấu '=' xảy ra khi x-2=0
hay x=2
Vậy: Gtnn của biểu thức \(\left(x-2\right)^2\) là 0 khi x=2
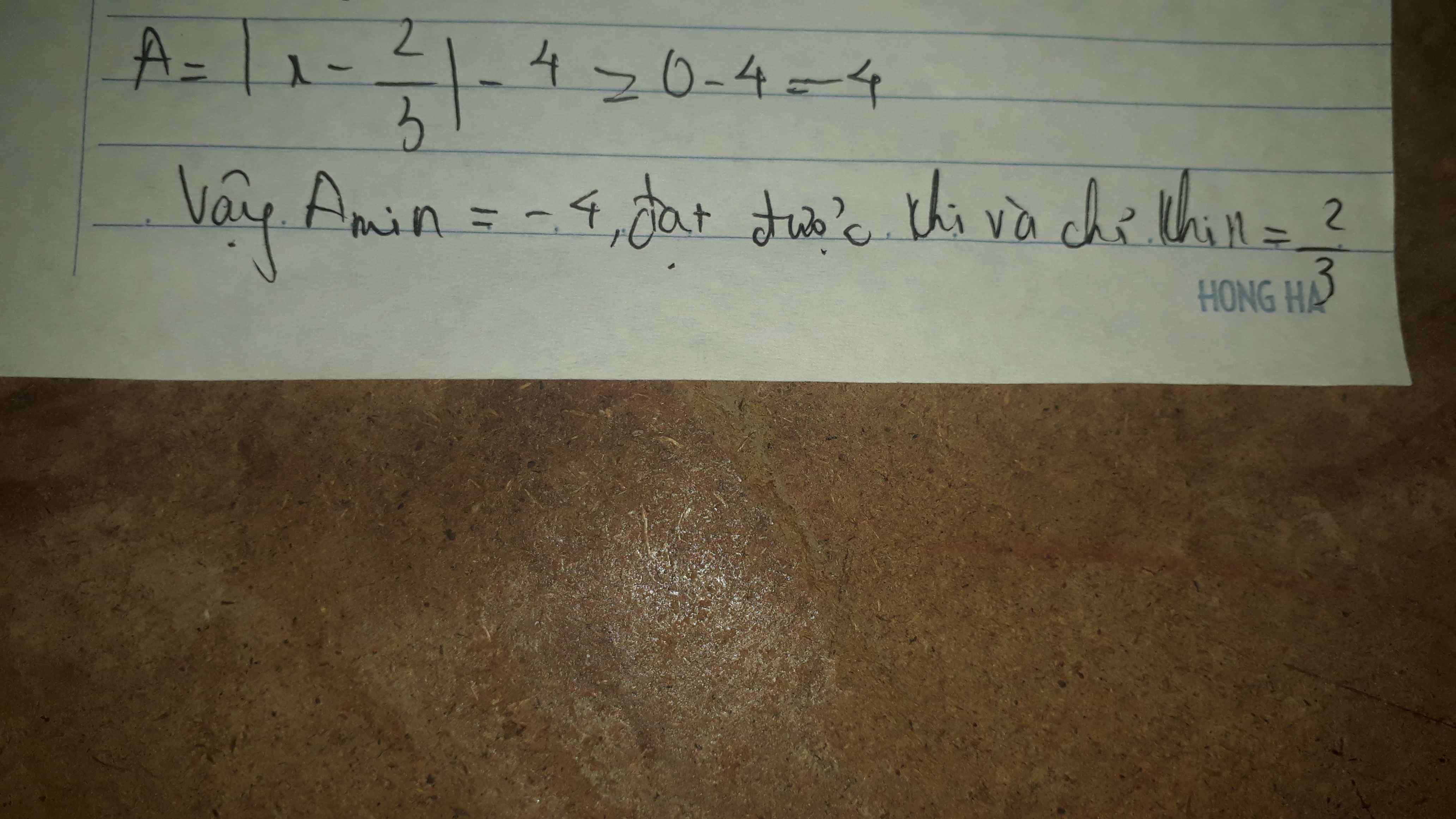
GTNN của A = 1 khi x= 29
GTLN của B = 4