AP
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
A
18 tháng 7 2019
A = x2 - 6x + 11
Nhập phương trình vào máy tính lặp 3 lần dấu =
GTNN của A = 3
B = 2x2 + 10x - 1
Nhập phương trình vào máy tính lặp 3 lần dấu =
GTNN của B = \(-\frac{5}{2}\)
C = 5x - x2
=> C = -x2 + 5x
Nhập phương trình vào máy tính lặp 3 lần dấu =
GTLN của C = \(\frac{5}{2}\)
ND
2
20 tháng 10 2016
A = 2x^2 +10x - 1
2A = 4x^2 + 20x -1
2A = (2x+5)2 - 26
A = (2x+5)2/2 - 13
A có GTNN thì (2x+5)2/2 = 0
2x+ 5 =0
x = -5/2
PT
1
CM
3 tháng 3 2019
2 x 2 + 10 - 1 = 2 x 2 + 5 x - 1 / 2 B = 2 x 2 + 2 . 5 / 2 x + 5 / 2 2 - 5 / 2 2 - 1 / 2 = 2 x + 5 / 2 2 - 25 / 4 - 2 / 4 = 2 x + 5 / 2 2 - 27 / 2 = 2 x + 5 / 2 2 - 27 / 2 V ì x + 5 / 2 2 ≥ 0 n ê n 2 x + 5 / 2 2 ≥ 0 ⇒ 2 x + 5 / 2 2 - 27 / 2 ≥ - 27 / 2
Suy ra: B ≥ - 27/2 .
B= -27/2 khi và chỉ khi x + 5/2 = 0 suy ra x = -5/2
Vậy B = -27/2 là giá trị nhỏ nhất tại x = - 5/2
17 tháng 7 2023
\(A=x^2-4x+20=x^2-4x+4+16=\left(x-2\right)^2+16\)
Do \(\left(x-2\right)^2\ge0\)
\(\Rightarrow\left(x-2\right)^2+16\ge16\)
\(\Rightarrow Min\left(A\right)=16\)
\(B=x^2-3x+7=x^2-3x+\dfrac{9}{4}-\dfrac{9}{4}+7=\left(x-\dfrac{3}{2}\right)^2+\dfrac{19}{4}\)
Do \(\left(x-\dfrac{3}{2}\right)^2\ge0\)
\(\Rightarrow\left(x-\dfrac{3}{2}\right)^2+\dfrac{19}{4}\ge\dfrac{19}{4}\)
\(\Rightarrow Min\left(B\right)=\dfrac{19}{4}\)
\(C=-x^2-10x+70=-\left(x^2+10x+25\right)+25+70=-\left(x-5\right)^2+95\)
Do \(-\left(x-5\right)^2\le0\)
\(\Rightarrow-\left(x-5\right)^2+95\le95\)
\(\Rightarrow Max\left(C\right)=95\)
\(D=-4x^2+12x+1=-\left(4x^2-12x+9\right)+9+1=-\left(2x-3\right)^2+10\)
Do \(-\left(2x-3\right)^2\le0\)
\(\Rightarrow-\left(2x-3\right)^2+10\le10\)
\(\Rightarrow Max\left(D\right)=10\)
AH
Akai Haruma
Giáo viên
26 tháng 7 2021
Lời giải:
$B=5x^2+2x-3=5(x^2+\frac{2}{5}x+\frac{1}{5^2})-\frac{16}{5}$
$=5(x+\frac{1}{5})^2-\frac{16}{5}$
$\geq 5.0-\frac{16}{5}=\frac{-16}{5}$
Vậy GTNN của $B$ là $\frac{-16}{5}$. Giá trị này đạt tại $x+\frac{1}{5}=0\Leftrightarrow x=-\frac{1}{5}$
---------------------------------
$C=-9x^2+5x+1=1-(9x^2-5x)$
$=\frac{61}{36}-[(3x)^2-2.3x.\frac{5}{6}+(\frac{5}{6})^2]$
$=\frac{61}{36}-(3x-\frac{5}{6})^2$
$\leq \frac{61}{36}$
Vậy gtln của $C$ là $\frac{61}{36}$. Giá trị này đạt tại $3x-\frac{5}{6}=0\Leftrightarrow x=\frac{5}{18}$
-----------------------
$D=16x^2-8x+12=(4x)^2-2.4x.1+1+11$
$=(4x-1)^2+11\geq 0+11=11$
Vậy gtnn của $D$ là $11$. Giá trị này đạt tại $4x-1=0\Leftrightarrow x=\frac{1}{4}$
LT
1
HT
28 tháng 12 2016
C = ( x2 - 4xy + 4y2 ) + 10.(x -2y) + ( y2 -2y + 1) + 27
= ( x-2y)2 + 2.5.(x-2y) + 25 + (y-1)2 + 2
= ( x-2y + 5 )2 + (y-1)2 + 2 \(\ge2\)vì \(\left(x-2y+5\right)^2\ge0\forall x,y\) và \(\left(y-1\right)^2\ge0\forall y\)
Dấu = xảy ra \(\Leftrightarrow\hept{\begin{cases}x-2y+5=0\\y-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-3\\y=1\end{cases}}\)
Vậy Min C = 2 \(\Leftrightarrow\hept{\begin{cases}x=-3\\y=1\end{cases}}\)
PT
1
CM
30 tháng 7 2018
A = 2 x 2 - 8 x - 10
= 2 x 2 - 4 x + 4 - 18 = 2 x - 2 2 - 18
Do 2 x - 2 2 ≥ 0 với mọi x ⇒ 2 x - 2 2 – 18 ≥ −18
A = -18 khi và chỉ khi x - 2 = 0 hay x = 2
Do đó giá trị nhỏ nhất của biểu thức A bằng -18 tại x = 2
ND
0
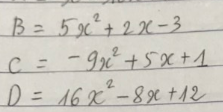
B=2x2+10x-1
=2(x2+5x-\(\frac{1}{2}\))
=2(x2+2x.\(\frac{5}{2}\)\(+\frac{25}{4}\)\(-\frac{27}{4}\))
=2[(x2+\(\frac{5}{2}\))2-\(\frac{27}{4}\)]
=2(x+\(\frac{5}{2}\))2-\(\frac{27}{2}\)\(\ge\frac{-27}{2}\)(vì (x+5/2)2\(\ge0\))
Dấu = xảy ra khi :
x+\(\frac{5}{2}\)=0
<=>x=\(\frac{-5}{2}\)
Vậy GTNN của B là \(\frac{-27}{2}\)khi x= \(\frac{-5}{2}\)
Tính GTNN của Biểu thức
2x2+40x-1