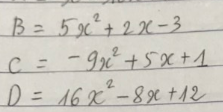ND
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
1
CW
20 tháng 10 2016
\(-5x^2+x-7=-5\left(x^2-\frac{1}{5}x+\frac{7}{5}\right)=-5\left(x^2-2\cdot\frac{1}{10}\cdot x+\frac{1}{100}-\frac{1}{100}+\frac{7}{5}\right)\)
\(=-5\left(x-\frac{1}{10}\right)^2+\frac{139}{20}\)
\(-5\left(x-\frac{1}{10}\right)^2+\frac{139}{20}\le\frac{139}{20}\)
GTLN của đa thức trên là 139/20
NP
0
ND
1
21 tháng 10 2016
A=...
dăt 5x=y viet cho gon
x=y/5
-A=y^2-y/5+3
=(y-1/10)^2+3-1/100
A=-(y-1/10)^2-299/100
GTLN=-299/100 khi y=1/10
BK
1
AH
Akai Haruma
Giáo viên
16 tháng 8 2021
Lời giải:
Ta có:
$x^2-3x+11=(x-\frac{3}{2})^2+\frac{35}{4}\geq \frac{35]{4}$
$\Rightarrow \frac{31}{x^2-3x+11}\leq 31:\frac{35}{4}=\frac{124}{35}$
$\Rightarrow \frac{31}{x^2-3x+11}+15\leq \frac{649}{35}$
Vậy gtln của biểu thức là $\frac{649}{35}$ khi $x=\frac{3}{2}$
BK
0
PT
1
CM
1 tháng 4 2019
C = 5 x - x 2 = - x 2 - 5 x = - x 2 - 2 . 5 / 2 x + 5 / 2 2 - 5 / 2 2 = - x - 5 / 2 2 - 25 / 4 = - x - 5 / 2 2 + 25 / 4 V ì - x - 5 / 2 2 ≤ 0 ⇒ - x - 5 / 2 2 + 25 / 4 ≤ 25 / 4
Suy ra: C ≤ 25/4 .
C = 25/4 khi và chỉ khi x - 5/2 = 0 suy ra x = 5/2
Vậy C = 25/4 là giá trị lớn nhất tại x = 5/2 .
AH
Akai Haruma
Giáo viên
26 tháng 7 2021
Lời giải:
$B=5x^2+2x-3=5(x^2+\frac{2}{5}x+\frac{1}{5^2})-\frac{16}{5}$
$=5(x+\frac{1}{5})^2-\frac{16}{5}$
$\geq 5.0-\frac{16}{5}=\frac{-16}{5}$
Vậy GTNN của $B$ là $\frac{-16}{5}$. Giá trị này đạt tại $x+\frac{1}{5}=0\Leftrightarrow x=-\frac{1}{5}$
---------------------------------
$C=-9x^2+5x+1=1-(9x^2-5x)$
$=\frac{61}{36}-[(3x)^2-2.3x.\frac{5}{6}+(\frac{5}{6})^2]$
$=\frac{61}{36}-(3x-\frac{5}{6})^2$
$\leq \frac{61}{36}$
Vậy gtln của $C$ là $\frac{61}{36}$. Giá trị này đạt tại $3x-\frac{5}{6}=0\Leftrightarrow x=\frac{5}{18}$
-----------------------
$D=16x^2-8x+12=(4x)^2-2.4x.1+1+11$
$=(4x-1)^2+11\geq 0+11=11$
Vậy gtnn của $D$ là $11$. Giá trị này đạt tại $4x-1=0\Leftrightarrow x=\frac{1}{4}$
