
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
$y=-2x^2+4x+3=5-2(x^2-2x+1)=5-2(x-1)^2$
Vì $(x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$ nên $y=5-2(x-1)^2\leq 5$
Vậy $y_{\max}=5$ khi $x=1$
Hàm số không có min.
Câu 2:
Hàm số $y$ có $a=-3<0; b=2, c=1$ nên đths có trục đối xứng $x=\frac{-b}{2a}=\frac{1}{3}$
Lập BTT ta thấy hàm số đồng biến trên $(-\infty; \frac{1}{3})$ và nghịch biến trên $(\frac{1}{3}; +\infty)$
Với $x\in (1;3)$ thì hàm luôn nghịch biến
$\Rightarrow f(3)< y< f(1)$ với mọi $x\in (1;3)$
$\Rightarrow$ hàm không có min, max.

Tham khảo:
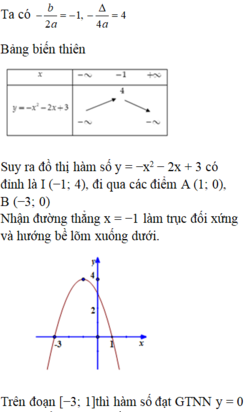
Đỉnh S có tọa độ: \({x_S} = \dfrac{{ - b}}{{2a}} = \dfrac{{ - 2}}{{2.1}} = - 1;\,{y_S} = {\left( { - 1} \right)^2} + 2.( - 1) + 3 = 2.\)
Hay \(S\left( { - 1;2} \right).\)
Vì hàm số bậc hai có \(a = 1 > 0\) nên ta có bảng biến thiên sau:
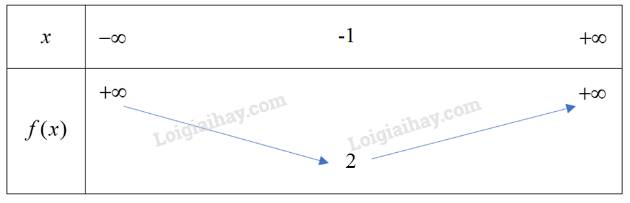
Hàm số đạt giá trị nhỏ nhất bằng \(2\).

Từ đề bài suy ra: 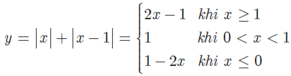
Bảng biến thiên
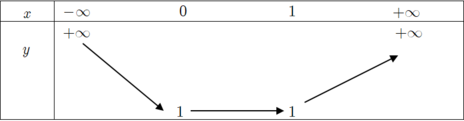
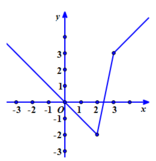
Ta có y(-2) =5; y(2) =3
Dựa vào bảng biến thiên ta có

Chọn D.

\(y=\sqrt{\left(x^2-2x+1\right)+4}=\sqrt{\left(x-1\right)^2+4}\ge\sqrt{4}=2\)
Đẳng thức xảy ra khi x = 1
Vậy min y = 2 khi x = 1

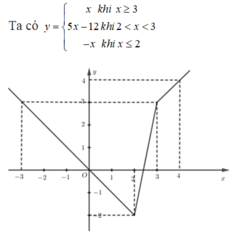
Ta có: 
+Vẽ đường thẳng y= x với x≥3 đi qua hai điểm O(0; 0) và A(1;1) và lấy phần đường thẳng bên phải của đường thẳng x= 3.
+Vẽ đường thẳng y=5x-12 với 2≤ x≤ 3 đi qua hai điểm B(3;3) và C( 2; -2) và lấy phần đường thẳng nằm giữa của hai đường thẳng x=2; x=3.
+Vẽ đường thẳng y= -x đi qua hai điểm O và D( -1; -1) và lấy phần đường thẳng bên trái của đường thẳng x= 2
+ Dựa vào đồ thị hàm số ta có:
![]()
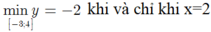
Chọn C.


\(y=2\left(x^2-4x+4\right)-3=2\left(x-2\right)^2-3\ge-3\)
\(y_{min}=-3\) khi \(x=2\)