Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) \(M=x^2-3x+10=\left(x^2-3x+\frac{9}{4}\right)+\frac{31}{4}\)
\(=\left(x-\frac{3}{2}\right)^2+\frac{31}{4}\ge\frac{31}{4}\left(\forall x\right)\)
Dấu "=" xảy ra khi: \(\left(x-\frac{3}{2}\right)^2=0\Rightarrow x=\frac{3}{2}\)
KL:...
2. a. \(A=12a-4a^2+3=-4\left(a-\frac{3}{2}\right)^2+12\)
Vì \(\left(a-\frac{3}{2}\right)^2\ge0\forall a\)\(\Rightarrow-4\left(a-\frac{3}{2}\right)^2+3\le3\)
Dấu "=" xảy ra \(\Leftrightarrow-4\left(a-\frac{3}{2}\right)^2=0\Leftrightarrow a-\frac{3}{2}=0\Leftrightarrow a=\frac{3}{2}\)
Vậy Amax = 3 <=> a = 3/2
b. \(B=4t-8v-v^2-t^2+2017=-\left(v^2+t^2-4t+8v+20\right)+2037\)
\(=-\left(t-2\right)^2-\left(v+4\right)^2+2037\)
Vì \(\left(t-2\right)^2\ge0;\left(v+4\right)^2\ge0\forall t;v\)
\(\Rightarrow-\left(t-2\right)^2-\left(v+4\right)^2+2037\le2037\)
Dấu "=" xảy ra \(\Leftrightarrow\orbr{\begin{cases}\left(t-2\right)^2=0\\\left(v+4\right)^2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}t-2=0\\v+4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}t=2\\v=-4\end{cases}}\)
Vậy Bmax = 2037 <=> t = 2 ; v = - 4
c. \(C=m-\frac{m^2}{4}=-\frac{1}{4}\left(m-2\right)^2+1\)
Vì \(\left(m-2\right)^2\ge0\forall m\)\(\Rightarrow-\frac{1}{4}\left(m-2\right)^2+1\le1\)
Dấu "=" xảy ra \(\Leftrightarrow-\frac{1}{4}\left(m-2\right)^2=0\Leftrightarrow m-2=0\Leftrightarrow m=2\)
Vậy Cmax = 1 <=> m = 2

a) Đặt A = u2 + v2 - 2u + 3v + 15
= (u2 - 2u + 1) + (v2 + 3v + 9/4) + 47/4
= (u - 1)2 + (v + 3/2)2 + 47/4 \(\ge\frac{47}{4}\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}u-1=0\\v+\frac{3}{2}=0\end{cases}}\Rightarrow\hept{\begin{cases}u=1\\v=-\frac{3}{2}\end{cases}}\)
Vậy Min A = 47/4 <=> u = 1 ; y = -3/2

a.
\(A=x^2-4x+4+2=\left(x-2\right)^2+2\ge2\)
GTNN của A đạt 2 khi và chỉ khi \(x=2\)
b.
\(B=y^2-2.\dfrac{1}{2}y+\dfrac{1}{4}+\dfrac{3}{4}=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
GTNN của B đạt \(\dfrac{3}{4}\) khi và chỉ khi \(y=\dfrac{1}{2}\)
c.
\(C=x^2-4x+4+y^2-2.\dfrac{1}{2}y+\dfrac{1}{4}+\dfrac{3}{4}\\ =\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
GTNN của C đạt \(\dfrac{3}{4}\) khi và chỉ khi \(\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)
a) \(A=x^2-4x+6\)
\(A=x^2-4x+4+2\)
\(A=\left(x-2\right)^2+2\)
Mà: \(\left(x-2\right)^2\ge0\forall x\) nên \(A=\left(x-2\right)^2+2\ge2\forall x\)
Dấu "=" xảy ra:
\(\left(x-2\right)^2+2=2\Leftrightarrow x-2=0\)
\(\Leftrightarrow x=2\)
Vậy: \(A_{min}=2\) khi \(x=2\)
b) \(B=y^2-y+1\)
\(B=y^2-2\cdot\dfrac{1}{2}\cdot y+\dfrac{1}{4}+\dfrac{3}{4}\)
\(B=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà: \(\left(y-\dfrac{1}{2}\right)^2\ge\forall x\) nên \(B=\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu "=" xảy ra:
\(\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=\dfrac{3}{4}\Leftrightarrow y-\dfrac{1}{2}=0\)
\(\Leftrightarrow y=\dfrac{1}{2}\)
Vậy \(B_{min}=\dfrac{3}{4}\) khi \(y=\dfrac{1}{2}\)
c) \(C=x^2-4x+y^2-y+5\)
\(C=x^2-4x+4+y^2-y+\dfrac{1}{4}+\dfrac{3}{4}\)
\(C=\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\)
Mà: \(\left\{{}\begin{matrix}\left(x-2\right)^2\ge0\forall x\\\left(y-\dfrac{1}{2}\right)^2\ge0\forall x\end{matrix}\right.\) nên
\(C=\left(x-2\right)^2+\left(y-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu "=" xảy ra:
\(\left\{{}\begin{matrix}x-2=0\\y-\dfrac{1}{2}=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)
Vậy: \(C_{min}=\dfrac{3}{4}\) khi \(\left\{{}\begin{matrix}x=2\\y=\dfrac{1}{2}\end{matrix}\right.\)

Đặt \(A=x^2-4x+y^2-8y+6\)
\(\Leftrightarrow A=x^2-4x+4+y^2-8y+16-14\)
\(\Leftrightarrow A=\left(x-2\right)^2+\left(y-4\right)^2-14\)
Vì \(\left(x-2\right)^2\ge0;\left(y-4\right)^2\ge0\)
\(\Rightarrow\left(x-2\right)^2+\left(y-4\right)^2-14\ge-14\)
Dấu = xảy ra khi \(\hept{\begin{cases}x-2=0\\y-4=0\end{cases}\Rightarrow}\hept{\begin{cases}x=2\\y=4\end{cases}}\)
Vậy Min A = -14 khi x=2;y=4
\(A=x^2-4x+y^2-8y+6=\left(x^2-2.x.2+2^2\right)+\left(y^2-2.y.4+4^2\right)+\left(6-4-16\right)\)
\(=\left(x-2\right)^2+\left(y-4\right)^2-14\ge-14\)
Vậy \(MinA=-14\Leftrightarrow\hept{\begin{cases}\left(x-2\right)^2=0\\\left(y-4\right)^2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x-2=0\\y-4=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=4\end{cases}}}\)

A= x(x+5)+3(x+5)+4 =x2+5x+3x+15+4 =x2+8x+19 =x2+2.4.x+16+3=(x+4)2+3
ta thay : (x+4)2>hoac = 0 suy ra Amin khi va chi khi x+4=0 suy ra x=-4
Vay Amin = 3 khi x=-4
B=x2-4x+4+y2-8y+16-14 =(x-2)2+(y-4)2-14
vi (x-2)2 va (y-4)2 lon hon hoac bang 0 suy ra Bmin khi va chi khi (x-2)2=0 va (y-4)2=0
tinh ra nhu cau a (ban tu lam nhe)
vay Bmin=-14 va x=2 va y=4

a) Từ M = x − 3 2 2 + 31 4 ≥ 31 4 ⇒ M min = 31 4 ⇔ x = 3 2 .
b) Ta có N = ( x + 2 y ) 2 + ( y – 2 ) 2 + ( x + 4 ) 2 – 120 ≥ - 120 .
Tìm được N min = -120 Û x = -4 và y = 2.

`A=x^2-4x+y^2-8y+6`
`A=x^2-4x+4+y^2-8y+16-14`
`A=(x-2)^2+(y-4)^2-14`
VÌ `(x-2)^2+(y-4)^2>=0`
`=>(x-2)^2+(y-4)^2-14>=-14`
`=>A>=-14`
Dấu "=" xảy ra khi `x-2=0,y-4=0<=>{(x=2),(y=4):}`
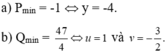

a) \(P=y^2+8y+15\)
\(P=y^2+2.y.4+16-1\)
\(P=\left(y+4\right)^2-1\)
Vì \(\left(y+4\right)^2\ge0\) với mọi y
\(\Rightarrow\left(y+4\right)^2-1\ge-1\) với mọi y
\(\Rightarrow Pmin=-1\Leftrightarrow y=-4\)
b) \(A=u^2+v^2-2u+3v+15\)
\(A=u^2-2u+1+v^2+2.v.\dfrac{3}{2}+\dfrac{9}{4}-\dfrac{9}{4}+14\)
\(A=\left(u-1\right)^2+\left(v+\dfrac{3}{2}\right)^2+\dfrac{47}{4}\)
Vì \(\left(u-1\right)^2\ge0\) với mọi u
\(\left(v+\dfrac{3}{2}\right)^2\ge0\) với mọi v
\(\Rightarrow\left(u-1\right)^2+\left(v+\dfrac{3}{2}\right)^2\ge0\) với mọi u,v
\(\Rightarrow\left(u-1\right)^2+\left(v+\dfrac{3}{2}\right)^2+\dfrac{47}{4}\ge\dfrac{47}{4}\)
\(\Rightarrow Amin=\dfrac{47}{4}\Leftrightarrow\left\{{}\begin{matrix}u=1\\v=-\dfrac{3}{2}\end{matrix}\right.\)