K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 11 2021
\(A=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\\ A_{min}=4\Leftrightarrow x=1\\ B=2\left(x^2-3x\right)=2\left(x^2-2\cdot\dfrac{3}{2}x+\dfrac{9}{4}\right)-\dfrac{9}{2}\\ B=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\\ B_{min}=-\dfrac{9}{2}\Leftrightarrow x=\dfrac{3}{2}\\ C=-\left(x^2-4x+4\right)+7=-\left(x-2\right)^2+7\le7\\ C_{max}=7\Leftrightarrow x=2\)
13 tháng 11 2021
a,\(A=x^2-2x+5=\left(x^2-2x+1\right)+4=\left(x-1\right)^2+4\ge4\)
Dấu "=" \(\Leftrightarrow x=-1\)
b,\(B=2\left(x^2-3x\right)=2\left(x^2-3x+\dfrac{9}{4}\right)-\dfrac{9}{2}=2\left(x-\dfrac{3}{2}\right)^2-\dfrac{9}{2}\ge-\dfrac{9}{2}\)
Dấu "=" \(\Leftrightarrow x=\dfrac{3}{2}\)
c,\(=C=-\left(x^2-4x-3\right)=-\left[\left(x^2-4x+4\right)-7\right]=-\left(x-2\right)^2+7\le7\)
Dấu "=" \(\Leftrightarrow x=2\)
5 tháng 2 2021
1, Ta có: 3-x2+2x=-(x2-2x+1)+4=-(x-1)2+4
vì (x-1)2 luôn lớn hơn hoặc bằng không với mọi x-->-(x-1)2 nhỏ hơn hoặc bằng 0 với mọi x
vậy giá trị lớn nhất của biểu thức 3-x2+2x là 4
5 tháng 2 2021
các bài giá trị nhỏ nhất còn lại làm tương tự bạn nhé
chỉ cần đưa về nhân tử chung hoặc hằng đẳng thức là được
23 tháng 10 2020
A = x2 - 2x + 9 = ( x2 - 2x + 1 ) + 8 = ( x - 1 )2 + 8 ≥ 8 ∀ x
Dấu "=" xảy ra khi x = 1
=> MinA = 8 <=> x = 1
B = x2 + 6x - 3 = ( x2 + 6x + 9 ) - 12 = ( x + 3 )2 - 12 ≥ -12 ∀ x
Dấu "=" xảy ra khi x = -3
=> MinB = -12 <=> x = -3
C = ( x - 1 )( x - 3 ) + 9 = x2 - 4x + 3 + 9 = ( x2 - 4x + 4 ) + 8 = ( x - 2 )2 + 8 ≥ 8 ∀ x
Dấu "=" xảy ra khi x = 2
=> MinC = 8 <=> x = 2
D = -x2 - 4x + 7 = -( x2 + 4x + 4 ) + 11 = -( x + 2 )2 + 11 ≤ 11 ∀ x
Dấu "=" xảy ra khi x = -2
=> MaxD = 11 <=> x = -2
20 tháng 7 2021
a, \(A=-x^2-2x+3=-\left(x^2+2x-3\right)=-\left(x^2+2x+1-4\right)\)
\(=-\left(x+1\right)^2+4\le4\)
Dấu ''='' xảy ra khi x = -1
Vậy GTLN là 4 khi x = -1
b, \(B=-4x^2+4x-3=-\left(4x^2-4x+3\right)=-\left(4x^2-4x+1+2\right)\)
\(=-\left(2x-1\right)^2-2\le-2\)
Dấu ''='' xảy ra khi x = 1/2
Vậy GTLN B là -2 khi x = 1/2
c, \(C=-x^2+6x-15=-\left(x^2-2x+15\right)=-\left(x^2-2x+1+14\right)\)
\(=-\left(x-1\right)^2-14\le-14\)
Vâỵ GTLN C là -14 khi x = 1
Bài 8 :
b, \(B=x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\)
Dấu ''='' xảy ra khi x = 3
Vậy GTNN B là 2 khi x = 3
c, \(x^2-x+1=x^2-x+\dfrac{1}{4}+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
Dấu ''='' xảy ra khi x = 1/2
Vậy ...
c, \(x^2-12x+2=x^2-12x+36-34=\left(x-6\right)^2-34\ge-34\)
Dấu ''='' xảy ra khi x = 6
Vậy ...
YN
30 tháng 6 2021
\(1.\)
\(-17-\left(x-3\right)^2\)
Ta có: \(\left(x-3\right)^2\ge0\)với \(\forall x\)
\(\Leftrightarrow-\left(x-3\right)^2\le0\)với \(\forall x\)
\(\Leftrightarrow17-\left(x-3\right)^2\le17\)với \(\forall x\)
Dấu '' = '' xảy ra khi:
\(\left(x-3\right)^2=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
Vậy \(Max=-17\)khi \(x=3\)
YN
30 tháng 6 2021
\(2.\)
\(A=x\left(x+1\right)+\frac{3}{2}\)
\(A=x^2+x+\frac{3}{2}\)
\(A=\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\)
\(\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
\(\Leftrightarrow\left(x+\frac{1}{2}\right)^2+\frac{5}{4}\ge\frac{5}{4}\)với \(\forall x\)
Vậy \(Max=\frac{5}{4}\)khi \(x=\frac{-1}{2}\)
T
8 tháng 9 2023
\(a,x^2+3x+9\)
\(=x^2+2\cdot x\cdot\dfrac{3}{2}+\left(\dfrac{3}{2}\right)^2+\dfrac{27}{4}\)
\(=\left(x+\dfrac{3}{2}\right)^2+\dfrac{27}{4}\)
Ta thấy: \(\left(x+\dfrac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+\dfrac{3}{2}\right)^2+\dfrac{27}{4}\ge\dfrac{27}{4}\forall x\)
Dấu \("="\) xảy ra \(\Leftrightarrow x+\dfrac{3}{2}=0\Leftrightarrow x=-\dfrac{3}{2}\)
\(b,2x^2-5x+10\)
\(=2x^2-5x+\dfrac{25}{8}+\dfrac{55}{8}\)
\(=2\left(x^2-2\cdot x\cdot\dfrac{5}{4}+\dfrac{25}{16}\right)+\dfrac{55}{8}\)
\(=2\left(x-\dfrac{5}{4}\right)^2+\dfrac{55}{8}\)
Ta có: \(2\left(x-\dfrac{5}{4}\right)^2\ge0\forall x\)
\(\Rightarrow2\left(x-\dfrac{5}{4}\right)^2+\dfrac{55}{8}\ge\dfrac{55}{8}\forall x\)
Dấu \("="\) xảy ra \(\Leftrightarrow x-\dfrac{5}{4}=0\Leftrightarrow x=\dfrac{5}{4}\)
#\(Toru\)
6 tháng 5 2020
\(A=\left[\frac{6x^2}{x^3-1}-\frac{2x-2}{x^2+x+1}-\frac{1}{x-1}\right]:\frac{x^2+9}{\left(x-1\right)\left(9-4x\right)}\)
\(=\left[\frac{6x^2}{x^3-1}-\frac{\left(2x-2\right)\left(x-1\right)}{\left(x^2+x+1\right)\left(x-1\right)}-\frac{x^2+x+1}{\left(x-1\right)\left(x^2+x+1\right)}\right]\cdot\frac{\left(x-1\right)\left(9-4x\right)}{x^2+9}\)
\(=\frac{6x^2-\left(2x^2-4x+2\right)-x^2-x-1}{\left(x^2+x+1\right)\left(x-1\right)}\cdot\frac{\left(x-1\right)\left(9-4x\right)}{x^2+9}\)
\(=\frac{5x^2-2x^2+4x-2-x-1}{\left(x^2+x+1\right)}\cdot\frac{\left(9-4x\right)}{x^2+9}\)
\(=\frac{3x^2+3x-3}{\left(x^2+x+1\right)}\cdot\frac{\left(9-4x\right)}{x^2+9}\)
Biểu thức A bạn viết đúng chưa?
LN
0
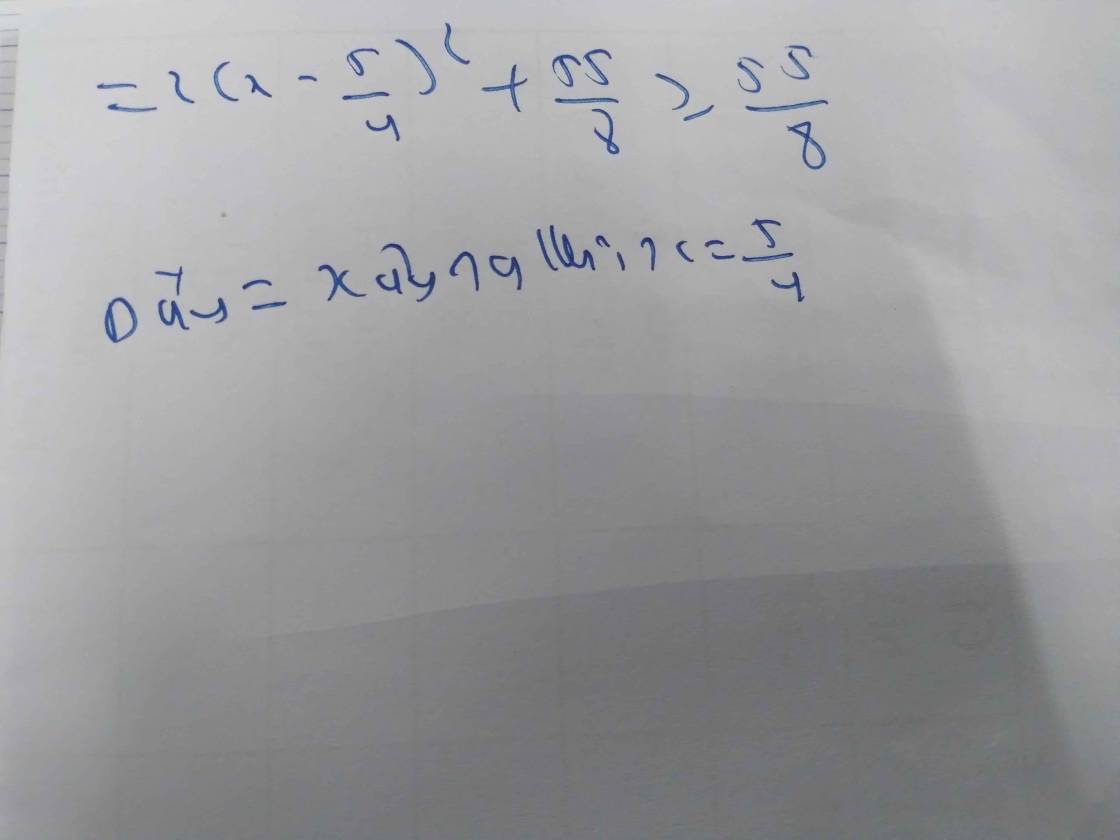
\(A=x^2-2x+9=x^2-2x+1+8=\left(x-1\right)^2+8\)
ta có: \(\left(x-1\right)^2\ge0\forall x\in R\)
\(\Rightarrow\left(x-1\right)^2+8\ge8\forall x\in R\)
dấu "=" xảy ra khi x - 1 = 0 => x = 1
vậy min A = 8 khi và chỉ khi x = 1