LC
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DC
0
14 tháng 9 2021
\(x^2+2xy+6x+6y+2y^2+8=0\\ \Leftrightarrow\left(x+y\right)^2+6\left(x+y\right)+y^2=-8\)
Ta có \(y^2\ge0\Leftrightarrow\left(x+y\right)^2+6\left(x+y\right)\le-8\)
\(\Leftrightarrow\left(x+y\right)^2+6\left(x+y\right)+9\le1\\ \Leftrightarrow\left(x+y+3\right)^2\le1\\ \Leftrightarrow\left|x+y+3\right|\le1\\ \Leftrightarrow-1\le x+y+3\le1\\ \Leftrightarrow2012\le B\le2014\)
\(B_{min}=2012\Leftrightarrow\left\{{}\begin{matrix}x+y+2016=2012\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=0\end{matrix}\right.\)
\(B_{max}=2014\Leftrightarrow\left\{{}\begin{matrix}x+y+2016=2014\\y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
5 tháng 2 2022
b: Tham khảo:
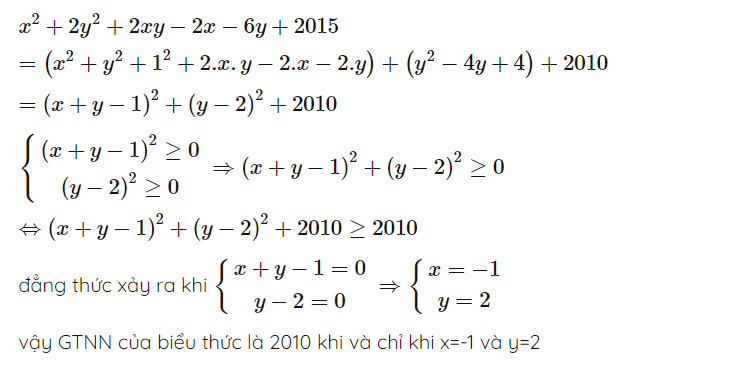
a: \(P=x^2-5x+\dfrac{25}{4}-\dfrac{25}{4}=\left(x-\dfrac{5}{2}\right)^2-\dfrac{25}{4}\ge-\dfrac{25}{4}\forall x\)
Dấu '=' xảy ra khi x=5/2
NN
0
3 tháng 3 2017
(x^2+y^2-12y-12x+36)+(5y^2-10y+5)+4=(x-y-6)^2+5(y-1)^2+4>=4
GTNN A=4
khi y=1
x=7
TT
15 tháng 2 2020
\(x^2+2xy+6x+6y+2y^2+8=0\)
\(\Leftrightarrow\left(x+y\right)^2+6\left(x+y\right)+9=1-y^2\)
\(\Leftrightarrow\left(x+y+3\right)^2=1-y^2\)
Ta thấy : \(1-y^2\le1\forall y\) \(\Rightarrow\left(x+y+3\right)^2\le1\)
\(\Rightarrow-1\le x+y+3\le1\)
\(\Rightarrow-1+2013\le x+y+3+2013\le1+2013\)
\(\Rightarrow2012\le x+y+2016\le2014\)
Vậy ta có :
+) Min \(B=2012\) . Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}y=0\\x+y+3=-1\end{cases}\Leftrightarrow}\hept{\begin{cases}y=0\\x=-4\end{cases}}\)
+) Max \(M=2014\). Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}y=0\\x+y+3=1\end{cases}\Leftrightarrow}\hept{\begin{cases}y=0\\x=-2\end{cases}}\)
HV
2
S
19 tháng 3 2020
\(N=2013-\left(x^2+2xy+y^2\right)-\left(y^2-6x+9\right)\)
\(N=2013-\left(x+y\right)^2-\left(y-3\right)^2\le2013-0-0=2013\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}y-3=0\\x+y=0\end{cases}}\Leftrightarrow\hept{\begin{cases}y=3\\x+3=0\end{cases}}\Leftrightarrow x=-3;y=3\)
DK
2
14 tháng 3 2018
<=> x^2 + 2x(y+2) + y^2+4y+4+y^2+2y+1-4
<=> x^2 + 2x(y+2) + (y+2)^2 + (y+1)^2 - 4
<=> (x+y+2)^2 + (y+1)^2 - 4 >= -4
min = -4 khi y = -1 , x = -1
14 tháng 3 2018
\(=\left(x+y+2\right)^2+\left(y+1\right)^2-4\)
Vì \(\left(x+y+2\right)^2\ge0\forall x\) , \(\left(y+1\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+y+2\right)^2+\left(y+1\right)^2\ge0\forall x\)
\(\Rightarrow\left(x+y+2\right)^2+\left(y+1\right)^2-4\ge-4\forall x\)
Vậy GTNN của A=-4 Dấu bằng xảy ra khi
\(\Rightarrow\hept{\begin{cases}\left(x+y+2\right)^2=0\\\left(y+1\right)^2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-2-y\\y=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-3\\y=-1\end{cases}}\)
Vậy GTNN của A=-4 khi và chỉ khi x=-3 , y=-1
Q = - x2 - 2y2 - 2xy + 8x + 6y + 13
= - x2 - y2 - 42 - 2xy + 8y + 8x - y2 - 2y - 1 + 30
= 30 - (x2 + y2 + 42 + 2xy - 8y - 8x) - (y2 + 2y + 1)
= 78 - (x + y - 4)2 - (y + 1 )2 \(\le\) 30
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x+y-4=0\\y+1=0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\)
\(Q=-x^2-2y^2-2xy+8x+6y+13\)
\(=-\left(x^2+2xy-8x\right)-2y^2+6y+13\)
\(=-\left[x^2+2x\left(y-8\right)+\left(y-8\right)^2\right]-2y^2+6y+13-\left(y-8\right)^2\)\(=-\left(x+y-8\right)^2-2y^2+6y+13-y^2+16y-64\)\(=-\left(x+y-8\right)^2-3y^2+22y-51\)
\(=-\left(x+y-8\right)^2-3\left(y^2-\dfrac{22}{3}y+\dfrac{121}{9}\right)-\dfrac{32}{3}\)\(=-\left(x+y-8\right)^2-3\left(y-\dfrac{11}{9}\right)^2-\dfrac{32}{3}\le-\dfrac{32}{2}\forall x\)Vậy Max Q = \(-\dfrac{32}{3}\) khi \(\left\{{}\begin{matrix}x+y-8=0\\y-\dfrac{11}{9}=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x-\dfrac{61}{9}=0\\y=\dfrac{11}{9}\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\dfrac{61}{9}\\y=\dfrac{11}{9}\end{matrix}\right.\)