BM
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
9 tháng 8 2016
Ta có : f(x) đạt giá trị lớn nhất <=> \(\frac{1}{f\left(x\right)}\) đạt giá trị nhỏ nhất
Xét : \(\frac{1}{f\left(x\right)}=\frac{x^2-2x+2016}{x^2}=\frac{2016}{x^2}-\frac{2}{x}+1\)
Đặt \(t=\frac{1}{x}\Rightarrow\frac{1}{f\left(x\right)}=2016t^2-2t+1=2016\left(t-\frac{1}{2016}\right)^2+\frac{2015}{2016}\ge\frac{2015}{2016}\)
\(\frac{1}{f\left(x\right)}\) đạt giá trị nhỏ nhất bằng \(\frac{2015}{2016}\)
Suy ra f(x) đạt giá trị lớn nhất bằng \(\frac{2016}{2015}\)
Dấu đẳng thức xảy ra khi và chỉ khi \(t=\frac{1}{2016}\Leftrightarrow x=2016\)
VH
0
28 tháng 2 2021
a,nghịch biến x<0
`<=>4m+2<0`
`<=>4m< -2`
`<=>m< -1/2`
`b,(4m+2)x^2<=0`
Mà `x^2>=0`
`<=>4m+2<0`
`<=>4m<-2`
`<=>m<-1/2`
28 tháng 2 2021
a) Để hàm số nghịch biến với mọi x<0 thì 4m+2>0
\(\Leftrightarrow4m>-2\)
hay \(m>-\dfrac{1}{2}\)
Vậy: Để hàm số nghịch biến với mọi x<0 thì \(m>-\dfrac{1}{2}\)
b) Để hàm số đạt giá trị lớn nhất là 0 thì 4m+2<0
hay \(m< -\dfrac{1}{2}\)
NV
1
CM
28 tháng 6 2017
Vẽ hình:
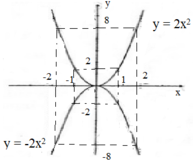
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
23 tháng 2 2021
Câu 1:
a) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(3m+5< 0\)
\(\Leftrightarrow3m< -5\)
hay \(m< -\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) nghịch biến với mọi x>0 thì \(m< -\dfrac{5}{3}\)
b) Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì
3m+5>0
\(\Leftrightarrow3m>-5\)
hay \(m>-\dfrac{5}{3}\)
Vậy: Để hàm số \(y=\left(3m+5\right)\cdot x^2\) đồng biến với mọi x>0 thì \(m>-\dfrac{5}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 2 2021
2.
Để hàm nghịch biến với x>0 \(\Leftrightarrow\sqrt{3k+4}-3< 0\)
\(\Leftrightarrow\sqrt{3k+4}< 3\Leftrightarrow3k+4< 9\)
\(\Rightarrow-\dfrac{4}{3}\le k< \dfrac{5}{3}\)
Để hàm đồng biến khi x>0
\(\Leftrightarrow\sqrt{3k+4}-3>0\Leftrightarrow\sqrt{3k+4}>3\)
\(\Leftrightarrow3k+4>9\Rightarrow k>\dfrac{5}{3}\)
22 tháng 2 2021
Câu 1:
a)
| \(y=f\left(x\right)=2x^2\) | -5 | -3 | 0 | 3 | 5 |
| f(x) | 50 | 18 | 0 | 18 | 50 |
b) Ta có: f(x)=8
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=8 thì \(x\in\left\{2;-2\right\}\)
Ta có: \(f\left(x\right)=6-4\sqrt{2}\)
\(\Leftrightarrow2x^2=6-4\sqrt{2}\)
\(\Leftrightarrow x^2=3-2\sqrt{2}\)
\(\Leftrightarrow x=\sqrt{3-2\sqrt{2}}\)
hay \(x=\sqrt{2}-1\)
Vậy: Để \(f\left(x\right)=6-4\sqrt{2}\) thì \(x=\sqrt{2}-1\)
Ta có f(x) đạt giá trị lớn nhất khi \(\frac{1}{f\left(x\right)}\) đạt giá trị nhỏ nhất.
Xét \(\frac{1}{f\left(x\right)}=\frac{x^2+2014x+1}{x}=x+\frac{1}{x}+2014\ge2\sqrt{x.\frac{1}{x}}+2014=2016\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}x>0\\x=\frac{1}{x}\end{cases}}\Leftrightarrow x=1\)
\(Min\)\(\frac{1}{f\left(x\right)}=2016\Leftrightarrow x=1\)
Vậy \(Max\)\(f\left(x\right)=\frac{1}{2016}\Leftrightarrow x=1\)