Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước 1: Tìm điều kiện của tham số để phương trình có hai nghiệm phân biệt.
Bước 2: Khi phương trình đã có hai nghiệm phân biệt, ta áp dụng Vi-ét để tìm các giá trị của tham số.
Bước 3. Đối chiếu với điều kiện và kết luận bài toán.
xem tr sách của anh
Bài 1:
PT có 2 nghiệm \(\Leftrightarrow\Delta=\left(m+2\right)^2-4\cdot2\ge0\Leftrightarrow m^2+4m-8\ge0\Leftrightarrow\left[{}\begin{matrix}m\le-2-2\sqrt{3}\\m\ge-2+2\sqrt{3}\end{matrix}\right.\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=m+2\\x_1x_2=2\end{matrix}\right.\)
Ta có \(\dfrac{x_1}{x_2}+\dfrac{x_2}{x_1}=\dfrac{9}{2}\Leftrightarrow2\left(x_1^2+x_2^2\right)=9x_1x_2\)
\(\Leftrightarrow2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]=18\\ \Leftrightarrow2\left(m+2\right)^2-8=18\\ \Leftrightarrow2m^2+8m+8-8=18\\ \Leftrightarrow m^2+4m-9=0\\ \Leftrightarrow\left[{}\begin{matrix}m=-2+\sqrt{13}\\m=-2-\sqrt{13}\end{matrix}\right.\left(tm\right)\)

Phương trình có 2 nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 13 4
⇔ a ≠ 0 Δ ≥ 0 − b a = 13 4 ⇔ m ≠ 0 m 2 − 3 3 − 4 m 2 ≥ 0 − m 2 − 3 m = 13 4
⇔ m ≠ 0 m 2 − 3 − 2 m m 2 − 3 + 2 m ≥ 0 4 m 2 + 13 m − 12 = 0
⇔ m ≠ 0 m + 1 m − 3 m − 1 m + 3 ≥ 0 m = 3 4 ; m = − 4
⇔ m ≠ 0 m ∈ − ∞ ; − 3 ∪ − 1 ; 1 ∪ 3 ; + ∞ m = 3 4 ; m = − 4 ⇔ m = 3 4 m = − 4
Vậy tổng bình phương các giá trị của m là: 265 16
Đáp án cần chọn là: A

Để phương trình có 2 nghiệm phân biệt :
\(\Delta>0< =>\left(-2\right)^2-4\left(-m\right)>0\)
\(< =>4+4m>0\)
\(< =>4m>-4\)
\(< =>m>-1\)
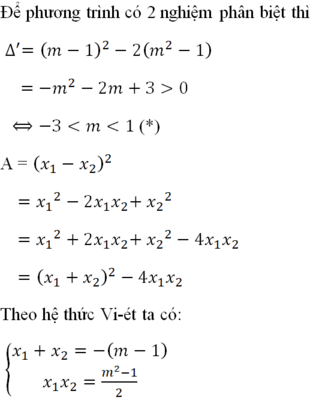
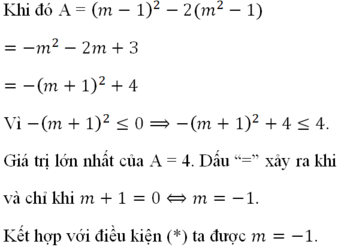
Để PT có 2 nghiệm \(\Leftrightarrow\Delta=\left[2\left(m+2\right)\right]^2-4\left(m^2+4\right)\ge0\)
\(\Leftrightarrow4m^2+16m+16-4m^2-16\ge0\\ \Leftrightarrow m\ge0\)
Áp dụng Viét: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+2\right)\\x_1x_2=m^2+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2\left(m+2\right)\left(1\right)\\x_1x_2=m^2+4\left(2\right)\\x_1+2x_2=7\left(3\right)\end{matrix}\right.\)
\(\left(3\right)-\left(1\right)=x_2=3-2m\)
Thay vào \(\left(1\right)\Leftrightarrow x_1=2\left(m+2\right)-x_2=2m+4-3+2m=4m+1\)
Thay vào \(\left(2\right)\Leftrightarrow\left(3-2m\right)\left(4m+1\right)=m^2+4\)
\(\Leftrightarrow10m+3-8m^2=m^2+4\\ \Leftrightarrow9m^2-10m+1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{1}{9}\end{matrix}\right.\left(tm\right)\)