
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án là D
• TH1: m = 0 ⇒ y ' = 3 > 0 , ∀ x ∈ ℝ thoả mãn.
• TH2: m ≠ 0 ,
Hàm số đã cho đồng biến trên ℝ khi và chỉ khi y ' = m x 2 − 2 m x + 3 ≥ 0 , ∀ x ∈ ℝ . ⇔ m > 0 m 2 − 3 m ≤ 0 ⇔ m > 0 0 ≤ m ≤ 3 ⇔ 0 < m ≤ 3 .
Vậy giá trị nhỏ nhất cần tìm m = 0.

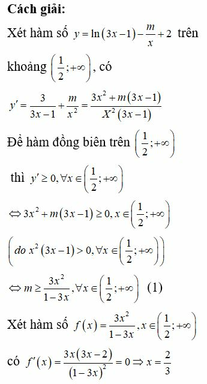

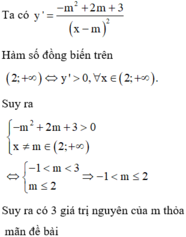




đúng nhé. em dựa theo lý thuyết bên trên ấy nhé
\(y'=3x^2-6x+m\)
để hàm số đồng biến trên R thì y'>0 với mọi x thuộc R
suy ra \(\begin{cases}3>0\\\Delta=9-3m