Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Do điểm M nằm trên trục hoành nên M( x; 0)
Khoảng cách từ M đến mỗi đường thẳng lần lượt là:
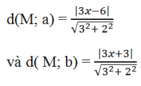
Theo bài ra ta có: d( M; a) = d( M; b) nên
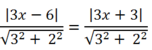
Do đó: ![]()
Sut ra 3x- 6= -3x-3 nên x= 1/2
Vậy điểm M ( 1/2; 0)

d: 4x-3y+5=0
=>VTPT là (4;-3) và (d) đi qua A(1;3)
=>VTCP là (3;4)
PTTS là:
x=1+3t và y=3+4t
=>N(3t+1;4t+3)
NM=1
=>\(\sqrt{\left(3t+1+1\right)^2+\left(4t+3-2\right)^2}=1\)
=>9t^2+12t+4+16t^2+8t+1=1
=>25t^2+20t+4=0
=>(5t+2)^2=0
=>t=-2/5
=>N(-1/5;-3/5)

a:
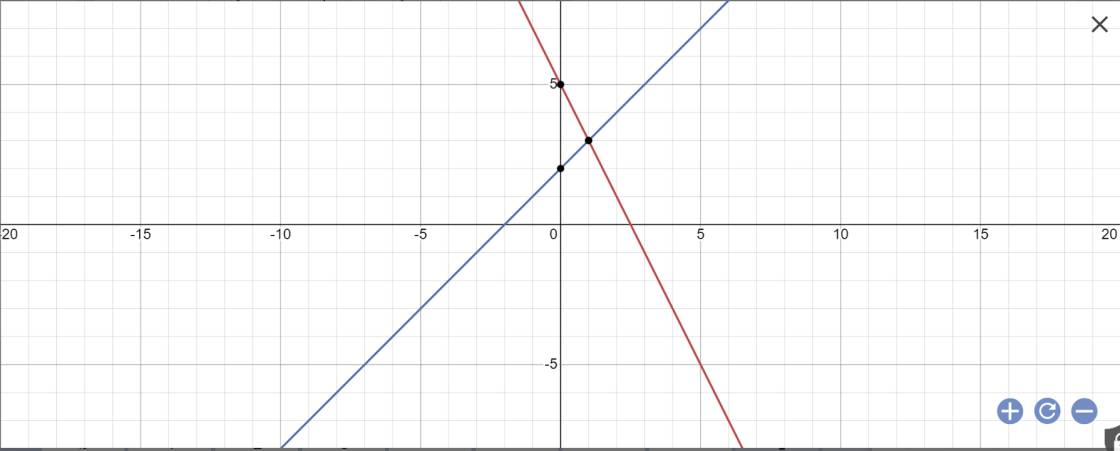
b: Phương trình hoành độ giao điểm là:
-2x+5=x+2
=>-2x-x=2-5
=>-3x=-3
=>x=1
Thay x=1 vào y=x+2, ta được;
y=1+2=3
Vậy: A(1;3)
c: Sửa đề: Tính góc tạo bởi đường thẳng y=x+2 với trục Ox
Gọi \(\alpha\) là góc tạo bởi đường thẳng y=x+2 với trục Ox
y=x+2 nên a=1
=>\(tan\alpha=a=1\)
=>\(\alpha=45^0\)
d: Vì (d)//y=-3x-1 nên \(\left\{{}\begin{matrix}a=-3\\b\ne-1\end{matrix}\right.\)
Vậy: (d): y=-3x+b
Thay x=1 và y=3 vào (d), ta được:
\(b-3\cdot1=3\)
=>b-3=3
=>b=6(nhận)
Vậy: (d): y=-3x+6

a: Thay x=3 và y=0 vào (1), ta được:
\(6-3m=0\)
hay m=2

Đáp án D
Ta gọi M(a ; 0)
Đường thẳng AB qua B(0 ; 3) và nhận A B → ( - 3 ; 4 ) làm VTCP và n → ( 4 ; 3 ) làm VTPT nên có pt :
4(x-0) + 3( y-3) =0 hay 4x + 3y -9= 0 và AB= 5
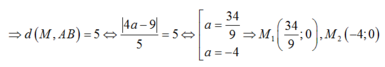

Gọi M( x; y) là giao điểm của đường thẳng (d) và trục hoành.
Khi đó; tọa độ điểm M là nghiệm hệ phương trình:
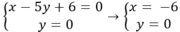
Vậy tọa độ điểm M( -6; 0) .
Chọn C.

Gọi M( x; y) là giao điểm của 2 đường thẳng (a) và (b) ( nếu có).
Khi đó; tọa độ điểm M là nghiệm hệ phương trình:
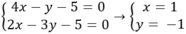
Vậy tọa độ giao điểm của 2 đường thẳng đã cho là : M( 1; -1)
Chọn C.

a) Từ phương trình tổng quát của đường thẳng, ta lấy được một vecto pháp tuyến là: \(\overrightarrow n = \left( {1; - 2} \right)\) nên ta chọn vecto chỉ phương của đường thẳng d là: \(\overrightarrow u = \left( {2;1} \right)\).
Chọn điểm \(A\left( {1; - 2} \right) \in d\).Vậy phương trình tham số của đường thẳng d là: \(\left\{ \begin{array}{l}x = 1 + 2t\\y = - 2 + t\end{array} \right.\) (t là tham số)
b) Do điểm M thuộc d nên ta có: \(M\left( {1 + 2m; - 2 + m} \right);m \in \mathbb{R}\).
Ta có: \(OM = 5 \Leftrightarrow \sqrt {{{\left( {1 + 2m} \right)}^2} + {{\left( { - 2 + m} \right)}^2}} = 5 \Leftrightarrow {m^2} = 4 \Leftrightarrow m = \pm 2\)
Với \(m = 2 \Rightarrow M\left( {5;0} \right)\)
Với \(m = - 2 \Rightarrow M\left( { - 3; - 4} \right)\)
Vậy ta có 2 điểm M thỏa mãn điều kiện đề bài.
c) Do điểm N thuộc d nên ta có: \(N\left( {1 + 2n; - 2 + n} \right)\)
Khoảng cách từ N đến trục hoành bằng giá trị tuyệt đối của tung độ điểm N. Do đó, khoảng cách tư N đến trục hoành bằng 3 khi và chỉ khi: \(\left| { - 2 + n} \right| = 3 \Leftrightarrow \left[ \begin{array}{l}n = 5\\n = - 1\end{array} \right.\)
Với \(n = 5 \Rightarrow N\left( {11;3} \right)\)
Với \(n = - 1 \Rightarrow N\left( { - 1; - 3} \right)\)
Vậy có 2 điểm N thỏa mãn bài toán
Gọi A(x;0) là điểm cần tìm
Theo đề, ta có: \(\dfrac{\left|x\cdot2+0\cdot\left(-3\right)-5\right|}{\sqrt{2^2+\left(-3\right)^2}}=\sqrt{37}\)
\(\Leftrightarrow\left|2x-5\right|=\sqrt{481}\)
=>\(\left[{}\begin{matrix}x=\dfrac{\sqrt{481}+5}{2}\\x=\dfrac{-\sqrt{481}+5}{2}\end{matrix}\right.\)