Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Từ định nghĩa bằng nhau của hai số phức, ta có:
a) ⇔
;
b) ⇔
;
c) ⇔
⇔
.

Do \(1\le x\le2\Rightarrow\left(x-1\right)\left(x-2\right)\le0\)
\(\Leftrightarrow x^2+2\le3x\)
Hoàn toàn tương tự ta có \(y^2+2\le3y\)
Do đó: \(P\ge\dfrac{x+2y}{3x+3y+3}+\dfrac{2x+y}{3x+3y+3}+\dfrac{1}{4\left(x+y-1\right)}\)
\(P\ge\dfrac{x+y}{x+y+1}+\dfrac{1}{4\left(x+y-1\right)}\)
Đặt \(a=x+y-1\Rightarrow1\le a\le3\)
\(\Rightarrow P\ge f\left(a\right)=\dfrac{a+1}{a+2}+\dfrac{1}{4a}\)
\(f'\left(a\right)=\dfrac{3a^2-4a-4}{4a^2\left(a+2\right)^2}=\dfrac{\left(a-2\right)\left(3a+2\right)}{4a^2\left(a+2\right)^2}=0\Rightarrow a=2\)
\(f\left(1\right)=\dfrac{11}{12}\) ; \(f\left(2\right)=\dfrac{7}{8}\) ; \(f\left(3\right)=\dfrac{53}{60}\)
\(\Rightarrow f\left(a\right)\ge\dfrac{7}{8}\Rightarrow P_{min}=\dfrac{7}{8}\) khi \(\left(x;y\right)=\left(1;2\right);\left(2;1\right)\)

\(\Leftrightarrow2y^3-6y^2+7y-3=-2x\sqrt{1-x}+2\sqrt{1-x}+\sqrt{1-x}\)
\(\Leftrightarrow2\left(y^3-3y^2+3y+1\right)+y-1=2\left(1-x\right)\sqrt{1-x}+\sqrt{1-x}\)
\(\Leftrightarrow2\left(y-1\right)^3+y-1=2\left(\sqrt{1-x}\right)^3+\sqrt{1-x}\) (1)
Xét hàm \(f\left(t\right)=2t^3+t\)
\(f'\left(t\right)=6t^2+1>0\Rightarrow f\left(t\right)\) đồng biến
Nên (1) tương đương: \(y-1=\sqrt{1-x}\Rightarrow y=1+\sqrt{1-x}\)
\(\Rightarrow P=x+2\sqrt{1-x}+2=-\left(1-x-2\sqrt{1-x}+1\right)+4=-\left(\sqrt{1-x}-1\right)^2+4\le4\)
⇒ P = x + 2 √ 1 − x + 2
= − ( 1 − x − 2 √ 1 − x + 1 ) + 4
= − ( √ 1 − x − 1 ) 2 + 4 ≤ 4
Cho xin một like đi các dân chơi à.


bài này mình chưa giải dc triệt để ở cái cuối
\(2x^3-4x^2+3x-1=2x^3\left(2-y\right)\sqrt{3-2y}\) \(\left(y\le\dfrac{3}{2}\right)\)
\(\Leftrightarrow4x^3-8x^2+6x-2=2x^3\left(4-2y\right)\sqrt{3-2y}\left(1\right)\)
\(đặt:\sqrt{3-2y}=a\ge0\Rightarrow a^2+1=4-2y\)
\(\left(1\right)\Leftrightarrow4x^3-8x^2+6x-2=2x^3.\left(a^2+1\right)a\)
\(\Leftrightarrow4x^3-8x^2+6x-2-2x^3\left(a^2+1\right)a\)
\(\Leftrightarrow-2\left(xa-x+1\right)\left[\left(xa\right)^2+x^2a+2x^2-xa-2x+1\right]=0\)
\(\Leftrightarrow x.a-x+1=0\Leftrightarrow x\left(a-1\right)=-1\Leftrightarrow x=\dfrac{-1}{a-1}\)
\(\left(\sqrt{x\sqrt{3-2y}-\sqrt{x}}\right) ^2=x\sqrt{3-2y}-\sqrt{x}\)
\(=\dfrac{-a}{a-1}-\sqrt{\dfrac{-1}{a-1}}\)
\(\left(\sqrt{x\sqrt{3-2y}+2}+\sqrt{x+1}\right)=\sqrt{\dfrac{-a}{a-1}+2}+\sqrt{\dfrac{a-2}{a-1}}\)
\(\Rightarrow\left(\dfrac{-a}{a-1}-\sqrt{-\dfrac{1}{a-1}}\right)\left(\sqrt{\dfrac{-a}{a-1}+2}+\sqrt{\dfrac{a-2}{a-1}}\right)-4=0\)
\(\Leftrightarrow\left(-\dfrac{a}{a-1}-\sqrt{-\dfrac{1}{a-1}}\right).2\sqrt{\dfrac{a-2}{a-1}}=4\)
\(\Leftrightarrow\left(-\dfrac{a}{a-1}-\sqrt{-\dfrac{1}{a-1}}\right)\sqrt{\dfrac{a-2}{a-1}}=2\)
\(\Leftrightarrow\left(-1+\dfrac{-1}{a-1}-\sqrt{-\dfrac{1}{a-1}}\right)\sqrt{1-\dfrac{1}{a-1}}=2\)(3)
\(đặt:1-\dfrac{1}{a-1}=u\Rightarrow\sqrt{-\dfrac{1}{a-1}}=\sqrt{u-1}\)
\(\left(3\right)\Leftrightarrow\left(u-2-\sqrt{u-1}\right)\sqrt{u}=2\)
bình phương lên tính được u
\(\Rightarrow u=.....\Rightarrow a\Rightarrow y=...\Rightarrow x=....\)
Với \(x=0\) không phải nghiệm
Với \(x>0\) chia 2 vế cho pt đầu cho \(x^3\)
\(\Rightarrow2-\dfrac{4}{x}+\dfrac{3}{x^2}-\dfrac{1}{x^3}=2\left(2-y\right)\sqrt{3-2y}\)
\(\Leftrightarrow1-\dfrac{1}{x}+\left(1-\dfrac{1}{x}\right)^3=\sqrt{3-2y}+\sqrt{\left(3-2y\right)^3}\)
Xét hàm \(f\left(t\right)=t+t^3\Rightarrow f'\left(t\right)=1+3t^2>0\Rightarrow f\left(t\right)\) đồng biến
\(\Rightarrow1-\dfrac{1}{x}=\sqrt{3-2y}\)
Thế vào pt dưới:
\(\left(\sqrt{x\left(1-\dfrac{1}{x}\right)-\sqrt{x}}\right)^2\left(\sqrt{x\left(1-\dfrac{1}{x}\right)+2}+\sqrt{x+1}\right)=4\)
\(\Leftrightarrow\left(x-\sqrt{x}-1\right)\left(\sqrt{x+1}+\sqrt{x+1}\right)=4\)
\(\Leftrightarrow\left(x-\sqrt{x}-1\right)\sqrt{x+1}=2\)
Phương trình này ko có nghiệm đẹp, chắc bạn ghi nhầm đề bài của pt dưới

\(4=2^x+2^y\ge2\sqrt{2^{x+y}}\Rightarrow2^{x+y}\le4\Rightarrow x+y\le2\)
\(\Rightarrow xy\le1\)
\(P=4x^2y^2+2x^3+2y^3+10xy\)
\(P=4x^2y^2+10xy+2\left(x+y\right)\left[\left(x+y\right)^2-3xy\right]\)
\(P\le4x^2y^2+10xy+4\left(4-3xy\right)=4x^2y^2-2xy+16\)
Đặt \(xy=t\Rightarrow0< t\le1\)
Xét hàm \(f\left(t\right)=4t^2-2t+16\) trên \((0;1]\)
\(\Rightarrow...\)
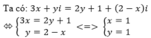
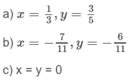
a)3x+yi=(2y+1)(2−x)i⇔{3x=2y+1y=2−x⇔{x=1y=13x+yi=(2y+1)(2−x)i⇔{3x=2y+1y=2−x⇔{x=1y=1
b)2x+y−1=(x+2y−5)i⇔{2x+y−1=0x+2y−5=0⇔{x=−1y=3