Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Để \(\dfrac{n+1}{n-2}\) có giá trị là một số nguyên thì n + 1 ⋮ n - 2
=> (n - 2) + 3 ⋮ n - 2
Vì (n - 2) ⋮ n - 2 nên 3 ⋮ n - 2
=> n - 2 ∈ Ư(3) ∈ {-3;-1;1;3}
=> n ∈ {-1;1;3;5}
b, Để \(\dfrac{4n+5}{2n-1}\) có giá trị là một số nguyên thì 4n + 5 ⋮ 2n - 1
=> (4n - 2) + 7 ⋮ 2n - 1
=> 2(2n - 1) + 7 ⋮ 2n - 1
Vì 2(2n - 1) ⋮ 2n -1 nên 7 ⋮ 2n - 1
=> 2n - 1 ∈ Ư(7) ∈ {-7;-1;1;7}
=> n ∈ {-3;0;1;4}

Để (3n+2)/(n-1) là số nguyên
=> 3n+2 chia hết cho n-1
=> (3n-3)+3+2 chia hết cho n-1
=>3(n-1)+5 chia hết cho n-1
Vì 3(n-1) chia hết cho n-1 nên 5 chia hết cho n-1
=> n-1 thuộc Ư(5)={-5;-1;1;5}
Nếu n-1=-5 => n=-4
Nếu n-1=-1 => n=0
Nếu n-1=1 => n=2
Nếu n-1=5 => n=6
Vậy n thuộc {-4;0;2;6}
:D

Do A có giá trị nguyên
\(\Rightarrow3n+2⋮n-1^{\left(1\right)}\)
Mà \(n-1⋮n-1\)
\(\Rightarrow3\left(n-1\right)⋮n-1^{\left(2\right)}\)
Từ (1) và (2)
\(\Rightarrow3n+2-3\left(n-1\right)⋮n-1\)
\(\Rightarrow3n+2-3n+3⋮n-1\)
\(\Rightarrow5⋮n-1\)
\(\Rightarrow n-1\inƯ\left(5\right)=\left\{-1;-5;5;1\right\}\)
Xét \(n-1=-1\Rightarrow n=-4\)
\(n-1=-5\Rightarrow n=0\)
\(n-1=5\Rightarrow n=6\)
\(n-1=1\Rightarrow n=2\)
Vậy ...
A = \(\frac{3n+2}{n-1}=\frac{3n-3+5}{n-1}=\frac{3\left(n-1\right)+5}{n-1}=\frac{3\left(n-1\right)}{n-1}+\frac{5}{n-1}=3+\frac{5}{n-1}\)
Để A có giá trị nguyên <=> n - 1 \(\in\)Ư(5) = {1;-1;5;-5}
Ta có: n - 1 = 1 => n = 2
n - 1 = -1 => n = 0
n - 1 = 5 => n = 6
n - 1 = -5 => n = -4
Vậy n = {2;0;6;-4}

a) Ta có:
Để A là phân số <=> n + 4 \(\ne\)0 <=> n \(\ne\)-4
b) Với : + )n = 1 => \(A=\frac{1+5}{1+4}=\frac{6}{5}\)
+) n = -1 => \(A=\frac{-1+5}{-1+4}=\frac{4}{3}\)
c) Ta có: \(A=\frac{n+5}{n+4}=\frac{\left(n+4\right)+1}{n+4}=1+\frac{1}{n+4}\)
Để A \(\in\)Z <=> 1 \(⋮\)n + 4
<=> n + 4 \(\in\)Ư(1) = {1; -1}
Lập bảng :
| n + 4 | 1 | -1 |
| n | -3 | -5 |
Vậy ....
1a) Để A là phân số thì n \(\ne\)- 4 ; n
b) + Khi n = 1
=> \(A=\frac{n+5}{n+4}=\frac{1+5}{1+4}=\frac{6}{5}\)
+ Khi n = -1
=> \(A=\frac{n+5}{n+4}=\frac{-1+5}{-1+4}=\frac{4}{3}\)
c) Để \(A\inℤ\)
=> \(n+5⋮n+4\)
=> \(n+4+1⋮n+4\)
Ta có : Vì \(n+4⋮n+4\)
=> \(1⋮n+4\)
=> \(n+4\inƯ\left(1\right)\)
=> \(n+4\in\left\{\pm1\right\}\)
Lập bảng xét các trường hợp
| \(n+4\) | \(1\) | \(-1\) |
| \(n\) | \(-3\) | \(-5\) |
Vậy \(A\inℤ\Leftrightarrow n\in\left\{-3;-5\right\}\)

Ta có
\(A=\frac{3n+4}{n-1}=3+\frac{7}{n-1}\)là số nguyên khi n-1 là ước của 7 hay
\(n-1\in\left\{\pm1,\pm7\right\}\Rightarrow n\in\left\{-6,0,2,8\right\}\)
Để A có giá trị nguyên
<=> 3n + 4 ⋮ n - 1
=> ( 3n - 3 ) + 7 ⋮ n - 1
=> 3 . ( n - 1 ) + 7 ⋮ n - 1
vì 3.(n-1) + 7 chia hết cho n-1 và 3.(n-1) chia hết cho n-1 nên 7 chia hết cho n-1
=> n - 1 ∈ Ư(7) = { - 7 ; -1 ; 1 ; 7 }
Ta có bảng sau :
| n-1 | 1 | -1 | -7 | 7 |
| n | 2 | 0 | -6 | 8 |
mọi giá trị n đều thuộc z (chọn)
Vậy x ∈ { - 6 ; 0 ; 2 ; 8 }

=> 3n + 2 là bội của n - 1 hay 3n + 2 phải chia hết cho n - 1
=> 3 là bội của n - 1 hay 3 phải chia hết cho n - 1
\(\RightarrowƯ_3=\left\{+-1;+-3\right\}\)
=> n - 1 = 1 => n = 1 + 1 = 2
n - 1 = -1 => n = -1 + 1 = 0
n - 1 = 3 => n = 3 + 1 = 4
n - 1 = -3 => n = -3 + 1 = -2
=> \(n\in\left\{-2;0;2;4\right\}\)

Để (3n+2)/(n-1) là số nguyên
=> 3n+2 chia hết cho n-1
=> (3n-3)+3+2 chia hết cho n-1
=>3(n-1)+5 chia hết cho n-1
Vì 3(n-1) chia hết cho n-1 nên 5 chia hết cho n-1
=> n-1 thuộc Ư(5)={-5;-1;1;5}
- Nếu n-1=-5 => n=-4
- Nếu n-1=-1 => n=0
- Nếu n-1=1 => n=2
- Nếu n-1=5 => n=6
Vậy n thuộc {-4;0;2;6}
Để (3n+2)/(n-1) là số nguyên
=> 3n+2 chia hết cho n-1
=> (3n-3)+3+2 chia hết cho n-1
=>3(n-1)+5 chia hết cho n-1
Vì 3(n-1) chia hết cho n-1 nên 5 chia hết cho n-1
=> n-1 thuộc Ư(5)={-5;-1;1;5}
- Nếu n-1=-5 => n=-4
- Nếu n-1=-1 => n=0
- Nếu n-1=1 => n=2
- Nếu n-1=5 => n=6
Vậy n thuộc {-4;0;2;6}

Để \(\frac{3n+2}{n-1}\)là số nguyên thì 3n + 2 phải chia hết cho n - 1
=> 3n - 3 + 5 chia hết cho n - 1
=> 3(n - 1) + 5 chia hết cho n - 1
=> 5 chia hết cho n - 1 (Vì 3(n - 1) chia hết cho n - 1)
=> n - 1 thuộc {-1; 1; -5; 5}
=> n thuộc {0; 2; -4; 6}
Vậy...
\(A=\frac{3n+2}{n-1}=\frac{3\left(n-1\right)+5}{n-1}=3+\frac{5}{n-1}\)
A E Z<=>5/n-1 E Z<=>5 chia hết chia hết cho n-1
=>n-1 E Ư(5)={-5;-1;1;5]
=>n E {-4;0;2;6}
vậy....
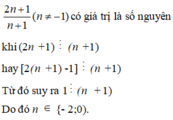
P số nào ? Đâu ?