Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có :
\(\frac{20a+13}{4a+3}=\frac{20a+15}{4a+3}-\frac{2}{4a+3}=5-\frac{2}{4a+3}\) đạt GTNN
<=> \(\frac{2}{4a+3}\) đạt GTLN <=> 4a + 3 đạt GTNN
Xét 4a + 3 > 0 vì nếu 4a + 3 < 0 thì \(\frac{2}{4a+3}<0\) do đó không thể đạt GTLN
Mà 4a + 3 > 0 đạt GTNN <=> 4a > 0 đạt GTNN <=> 4a = 0 <=> a = 0
Vậy a = 0

\(M=\frac{6n-3}{4n-6}=\frac{6n-9+6}{4n-6}=\frac{3\left(2n-3\right)}{2\left(2n-3\right)}+\frac{6}{4n-6}=\frac{3}{2}+\frac{6}{4n-6}\)
Do đó, để M có giá trị lớn nhất thì 6/(4n-6) có giá trị lớn nhất
=>4n-6 có giá trị nhỏ nhất(nEN)
=>4n-6=2
4n=6+2
4n=8
n=8/4=2
Nếu n=2 thì M=\(\frac{3}{2}+\frac{6}{4\cdot2-6}=\frac{3}{2}+\frac{6}{8-6}=\frac{3}{2}+3=\frac{3}{2}+\frac{6}{2}=\frac{9}{2}=4,5\)
Vậy M đạt giá trị lớn nhất là 4,5 tại n=2

Ta có y = x 2 + 2 x + a - 4 = x + 1 2 + a - 5
Đặt u = x + 1 2 khi đó ∀ x ∈ - 2 ; 1 thì u ∈ 0 ; 4
Ta được hàm số f u = u + a - 5
Khi đó
M a x x ∈ - 2 ; 1 y = M a x x ∈ 0 ; 4 f u = M a x f 0 , f 4 = M a x a - 5 ; a - 1
Trường hợp 1:
a - 5 ≤ a - 1 ⇔ a ≤ 3 ⇒ M a x x ∈ 0 ; 4 f u = 5 - a ≥ 2 ⇔ a = 3
Trường hợp 2:
a - 5 ≤ a - 1 ⇔ a ≥ 3 ⇒ M a x x ∈ 0 ; 4 f u = a - 1 ≥ 2 ⇔ a = 3
Vậy giá trị nhỏ nhất của M a x x ∈ - 2 ; 1 y = 2 ⇔ a = 3
Đáp án A

Đáp án A
Xét phương trình hoành độ giao điểm:
x + 1 2 x + 1 = m x + m + 1 2 ⇔ 4 m x 2 + 4 m x + m − 1 = 0 1
Phương trình (1) có 2 nghiệm x A ; x B ⇔ Δ ' = 4 m 2 − 4 m m − 1 = 4 m > 0 ⇔ m > 0.
Khi đó giao điểm của 2 đồ thị là A x A ; m x A + m + 1 2 ; B x B ; m x B + m + 1 2
với x A + x B = − 1 ; x A . x B = m − 1 4 m
Ta có O A 2 + O B 2 = x A 2 + m x A + m + 1 2 2 + x B 2 + m x B + m + 1 2 2 = m 2 + 2 m + 1 2 m = 1 + 1 2 m + 1 m ≥ 1 + 1 2 .2 = 2
( vì m > 0 , theo Cauchy ta có m + 1 m ≥ 2 . Dấu bằng xảy ra khi m = 1

Đáp án A
f x = 4 sin x + 6 m + sin x 9 sin x + 4 1 + sin x = 2 3 2 sin x + 6 m . 2 3 sin x 1 + 4. 2 3 2 sin x ,
đặt t = 2 3 sin x
⇒ f t = t 2 + n t 1 + 4 t 2 với 2 3 ≤ t ≤ 3 2 n = 6 m > 0
Bài toán trở thành tìm n >0 để f t ≥ 1 3 với t ∈ 2 3 ; 3 2
⇒ f t ≥ 1 3 ⇔ t 2 + n t 1 + 4 t 2 ≥ 1 3 ⇔ n ≥ t 3 + 1 3 t
Xét g t = t 3 + 1 3 t trên đoạn 2 3 ; 3 2 có min 2 3 ; 3 2 t = g 1 = 2 3
Theo bài ra ⇒ g t ≤ n phải có nghiệm trên 2 3 ; 3 2
⇔ n ≥ min 2 3 ; 3 2 g t ⇔ n ≥ 2 3 ⇔ m ≥ log 6 2 3

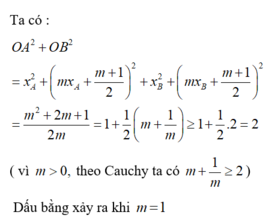

Để \(\frac{20+13}{4a+3}=\frac{33}{4a+3}\) đạt giá trị nhỏ nhất thì 4a+3 đạt giá trị nhỏ nhất và \(33\left(4a+3\right)\ge0\)
\(\Rightarrow4a\) đạt giá trị nhỏ nhất là số nguyên dương
\(\Rightarrow a=0\)
0