Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để số A chia hết cho 2,5 thì b = 0
Tổng các chữ số của số A là :
6 +1 + 4 = 11
Vậy a = 7 để A chia hết cho 2,3,5,9
Thử lại : 67140 chia hết cho 2,5
6 + 7 + 1 + 4 = 18
Mà 18 chia hết cho 3,9 nên số A bằng 67140 là đúng
Giải thích các bước giải:
A= 6a14b
Để A chia hết cho cả 2 và 5 ⇒ D tận cùng là 0
⇒ A= 6a140
Để A chia hết cho cả 3 và 9
⇒ Tổng các chữ số của A chia hết cho 9
hay 6+a+1 + 4 +0 =11 + a chia hết cho 9
=> a = 7
Vậy A = 67140
Để B = 25a1b chia hết cho 15
⇒ B chia hết cho 5 và cho 3
Vì B chia hết cho 5 nhưng k chia hếo 2 nênB tận cùng bằng chữ số 5
Hay B = 25a15
Để B chia hết cho 3 thì 2 + 5 + a + 1 + 5 = 13+a chia hết cho 3
⇒ a ∈ {2;5;8}
Vậy B có thể là 25215; 25515; 25815

a, Để 42ab chia hết cho 5 thì b = 0 hoặc b = 5.
TH1: b = 0 => 42ab = 42a0
Xét số 42a0 chia hết cho 9 khi ( 4 + 2 + a + 0 ) chia hết cho 9
hay ( 6 + a ) chia hết cho 9
=> a = 3.
TH2: b = 5 => 42ab = 42a5
Xét số 42a5 chia hết cho 9 khi ( 4 + 2 + a + 5 ) chia hết cho 9
hay ( 11 + a ) chia hết cho 9
=> a = 7.
Vậy a = 3 và b = 0 hoặc a = 7 và b = 5.
b, Vì 25a1b chia hết cho 5 nhưng không chia hết cho 2 => b = 5.
=> 25a1b = 25a15
Xét số 25a15 chia hết cho 3 khi ( 2 + 5 + a + 1 + 5 ) chia hết cho 3
hay ( 13 + a ) chia hết cho 3
=> a = 2 hoặc a = 5 hoặc a = 8.
Vậy b = 5 và a = 2 hoặc 5 hoặc 8.
c, Vì 45 = 9 x 5
=> 71a1b chia hết cho cả 9 và 5
=> b = 0 hoặc b = 5.
TH1: b = 0 => 71a1b = 71a10
Xét số 71a10 chia hết cho 9 khi ( 7 + 1 + a + 1 + 0 ) chia hết cho 9
hay ( 9 + a ) chia hết cho 9
=> a = 0 hoặc a = 9.
TH2: b = 5 => 71a1b = 71a15
Xét số 71a15 chia hết cho 9 khi ( 7 + 1 + a + 1 + 5 ) chia hết cho 9
hay ( 14 + a ) chia hết cho 9
=> a = 4.
Vậy b = 0 thì a = 0 hoặc 9 ; b = 5 thì a = 4.
d,579abc = 579000 + abc
Vì 579000 chia 7 dư 2 => abc chia 7 dư 5. => abc = 7k + 5 ( k \(\in\)N ) => 2 x abc - 3 = 14k + 7 chia hết cho 7 < 1 >
Vì 579000 chia 9 dư 3 => abc chia 9 dư 6. => abc = 9m + 6 ( m \(\in\)N ) => 2 x abc - 3 = 18m + 9 chia hết cho 9 < 2 >
Vì 579000 chia hết cho 5 => abc chia hết cho 5.
Từ < 1 > ; < 2 > => 2 x abc - 3 chia hết cho cả 9 và 7 mà ( 9,7 ) = 1 => 2 x abc - 3 chia hết cho 63
Để abc chia hết cho 5 => c = 0 hoặc 5 => 2 x abc - 3 có chữ số tận cùng là 7.
2 x abc có tận cùng là 7 và chia hết cho 63 => Thương của 2 x abc khi chia cho 63 chỉ có thể là 9; 19; 29; 39; 49; ...
Xét lần lượt thương là 9; 19; 29 ta tìm được abc = 285 hoặc 600 hoặc 915.
Vậy \(\left(a;b;c\right)\in\left\{\left(2;8;5\right);\left(6;0;0\right);\left(9;1;5\right)\right\}.\)
a) 42ab chia hết cho 9 và 5
Ta có: 42ab chia hết cho 5 nên 42ab có tận cùng là 0 hoặc 5, suy ra b có thể là 0 hoặc 5
Số chia hết cho 9 là số có tổng các chữ số chia hết cho 9
Để 42a0 chia hết cho 9 thì 4 + 2 + a + 0 chia hết cho 9 => a = 3 ( Vì 9 - 4 - 2 - 0 = 3)
Để 42a5 chia hết cho 9 thì 4 + 2 + a + 5 chia hết cho 9 => a = 7 ( Vì 18 - 4 - 2 - 5 = 7)
Vậy ta có hai số 4230 và 4275 chia hết cho 9 và 5
b) 25a1b chia hết cho 3, cho 5 và không chia hết cho 2
Số chia hết cho 5 và không chia hết cho 2 có tận cùng là 5 => b = 5 => số có dạng: 25a15
Số chia hết cho 3 là số có tổng các chữ số chia hết cho 3
Ta có 2 + 5 + 1 + 5 = 13 nên a có thể là các số: 2, 5, 8 ( lấy 15 - 13 =2; 18 - 13 = 5; 21 - 13 =8 )
c, d tương tự

a) (b = 0; a = 4); (b = 2; a = 2);(b = 4; a = 0); (b = 4; a = 9).
b) (b = 0; a = 0); b= 0; a = 9); (b = 5; a = 4).
c) (b = 0; a= 7).
d) (b = 5; a = 2); (b = 5;a = 5); (b = 5;a = 8).

\(B⋮̸12\Leftrightarrow b\in\left\{1;3;5;7;9\right\}\\ B⋮15\Leftrightarrow B⋮3;B⋮5\Leftrightarrow b\in\left\{0;5\right\}\\ \Leftrightarrow b=5\\ \Leftrightarrow B=\overline{25a15}⋮3\Leftrightarrow2+5+a+1+5⋮3\\ \Leftrightarrow13+a⋮3\\ \Leftrightarrow a\in\left\{2;5;8\right\}\)
Vậy \(B\in\left\{25215;25515;25815\right\}\)

a) (b = 0; a = 4); (b = 2; a = 2);(b = 4; a = 0); (b = 4; a = 9).
b) (b = 0; a = 0); b= 0; a = 9); (b = 5; a = 4).
c) (b = 0; a= 7).
d) (b = 5; a = 2); (b = 5;a = 5); (b = 5;a = 8).

Bài 4: Để tìm các chữ số a, b thỏa mãn các điều kiện, ta sẽ kiểm tra từng trường hợp.
a. Để số 4a12b chia hết cho 2, 5 và 9, ta cần xét chữ số cuối cùng b. Vì số chia hết cho 2, nên b phải là số chẵn. Vì số chia hết cho 5, nên b phải là 0 hoặc 5. Vì số chia hết cho 9, nên tổng các chữ số trong số đó phải chia hết cho 9. Ta thử từng trường hợp:
- Nếu b = 0, thì tổng các chữ số là 4 + a + 1 + 2 + 0 = 7 + a. Để 7 + a chia hết cho 9, ta có a = 2.
- Nếu b = 5, thì tổng các chữ số là 4 + a + 1 + 2 + 5 = 12 + a. Để 12 + a chia hết cho 9, ta có a = 6.
Vậy, các giá trị thỏa mãn là a = 2 hoặc a = 6, và b = 0 hoặc b = 5.
b. Để số 5a43b chia hết cho 2, 3 và 5, ta cần xét chữ số cuối cùng b. Vì số chia hết cho 2, nên b phải là số chẵn. Vì số chia hết cho 3, nên tổng các chữ số trong số đó phải chia hết cho 3. Vì số chia hết cho 5, nên b phải là 0 hoặc 5. Ta thử từng trường hợp:
- Nếu b = 0, thì tổng các chữ số là 5 + a + 4 + 3 + 0 = 12 + a. Để 12 + a chia hết cho 3, ta có a = 0 hoặc a = 3 hoặc a = 6 hoặc a = 9.
- Nếu b = 5, thì tổng các chữ số là 5 + a + 4 + 3 + 5 = 17 + a. Để 17 + a chia hết cho 3, ta có a = 1 hoặc a = 4 hoặc a = 7.
Vậy, các giá trị thỏa mãn là a = 0 hoặc a = 3 hoặc a = 6 hoặc a = 9, và b = 0 hoặc b = 5.
c. Để số 735a2b chia hết cho 5 và 9, nhưng không chia hết cho 2, ta cần xét chữ số cuối cùng b. Vì số chia hết cho 5, nên b phải là 0 hoặc 5. Vì số chia hết cho 9, nên tổng các chữ số trong số đó phải chia hết cho 9. Ta thử từng trường hợp:
- Nếu b = 0, thì tổng các chữ số là 7 + 3 + 5 + a + 2 + 0 = 17 + a. Để 17 + a chia hết cho 9, ta có a = 7 hoặc a = 8.
- Nếu b = 5, thì tổng các chữ số là 7 + 3 + 5 + a + 2 + 5 = 22 + a. Để 22 + a chia hết cho 9, ta có a = 2 hoặc a = 5 hoặc a = 8.
Vậy, các giá trị thỏa mãn là a = 2 hoặc a = 5 hoặc a = 7 hoặc a = 8, và b = 0 hoặc b = 5.
Bài 5: Để xác định xem tổng A có chia hết cho 8 hay không, ta cần tính tổng A và kiểm tra xem nó có chia hết cho 8 hay không.
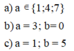
A) 4230, 4275
B) 25215,25515, 25815
chuc ban hoc tot
để 42ab \(⋮5\)thì b phải\(\in\left\{0;5\right\}\)
ta có 2 trường hợp
TH 1:
b=5
để \(42a5⋮9\)
thì các chữ số của nó cộng lại phải \(⋮9\)
4+2+5=11 mà \(18⋮9\)
vậy a là:
18-11=9
vậy a=9 khi có b=5
TH2:b=0
để \(42a0⋮9\)thì tổng các chữ số của nó\(⋮9\)
mà 9\(⋮9\)
a=9-(4+2)=3
vậy a=3 khi b=0
vậy 42ab \(\in\left\{4230;4295\right\}\)