
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(2x+5\sqrt{x}-7=2\left[\left(x+\dfrac{5}{2}\sqrt{x}+\dfrac{25}{16}\right)-\dfrac{25}{16}-\dfrac{7}{2}\right]\)
\(=2\left[\left(\sqrt{x}+\dfrac{5}{4}\right)^2-\dfrac{81}{16}\right]=2\left(\sqrt{x}+\dfrac{5}{4}-\dfrac{9}{4}\right)\left(\sqrt{x}+\dfrac{5}{4}+\dfrac{9}{4}\right)=2\left(\sqrt{x}-1\right)\left(\sqrt{x}+\dfrac{7}{2}\right)\)
2) \(3x-7\sqrt{x}+4=3\left[\left(x-\dfrac{7}{3}\sqrt{x}+\dfrac{49}{36}\right)-\dfrac{49}{36}+\dfrac{4}{3}\right]\)
\(=3\left[\left(\sqrt{x}-\dfrac{7}{6}\right)^2-\dfrac{1}{36}\right]=3\left(\sqrt{x}-\dfrac{7}{6}-\dfrac{1}{6}\right)\left(\sqrt{x}-\dfrac{7}{6}+\dfrac{1}{6}\right)=3\left(\sqrt{x}-\dfrac{4}{3}\right)\left(\sqrt{x}-1\right)\)
3) \(4x-4\sqrt{x}-8=4\left[\left(x-\sqrt{x}+\dfrac{1}{4}\right)-\dfrac{1}{4}-2\right]\)
\(=4\left[\left(\sqrt{x}-\dfrac{1}{2}\right)^2-\dfrac{9}{4}\right]=4\left(\sqrt{x}-\dfrac{1}{2}-\dfrac{3}{2}\right)\left(\sqrt{x}-\dfrac{1}{2}+\dfrac{3}{2}\right)=4\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)
| \(2x+5\sqrt{x}-7=\left(\sqrt{x}-1\right)\left(2\sqrt{x}+7\right)\) |
| \(3x-7\sqrt{x}+4=\left(3\sqrt{x}-4\right)\left(\sqrt{x}-1\right)\) |
| \(4x-4\sqrt{x}-8=\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\) |

`11+4sqrt6=8+2.2sqrt2.sqrt3+3=(2sqrt2+sqrt3)^2`
`11-4sqrt6=8-2.2sqrt2.sqrt3+3=(2sqrt2-sqrt3)^2`
`13+4sqrt10=8+2.2sqrt2.sqrt5+5=(2sqrt2+sqrt5)^2`
`13-4sqrt10=8-2.2sqrt2.sqrt5+5=(2sqrt2-sqrt5)^2`

\(5+2\sqrt{6}=\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}\)
\(6+2\sqrt{5}=\sqrt{\left(\sqrt{5}+1\right)^2}\)
\(5+2\sqrt{6}=\left(\sqrt{3}+\sqrt{2}\right)^2\)
\(6+2\sqrt{5}=\left(\sqrt{5}+1\right)^2\)

`12+2sqrt35=7+2sqrt{7.5}+5=(sqrt7+sqrt5)^2`
`9+4sqrt2=8+2.2sqrt2+1=(2sqrt2+1)^2`
`9-4sqrt2=8-2.2sqrt2+1=(2sqrt2-1)^2`
\(12+2\sqrt{35}=\left(\sqrt{7}+\sqrt{5}\right)^2\)
\(9+4\sqrt{2}=\left(2\sqrt{2}+1\right)^2\)
\(9-4\left(\sqrt{2}\right)=\left(2\sqrt{2}-1\right)^2\)

\(P=\dfrac{x+\sqrt{x}}{3\sqrt{x}-1}=\dfrac{7-4\sqrt{3}+\sqrt{7-4\sqrt{3}}}{3\sqrt{7-4\sqrt{3}}-1}=\dfrac{7-4\sqrt{3}+\sqrt{\left(2-\sqrt{3}\right)^2}}{3\sqrt{\left(2-\sqrt{3}\right)^2}-1}=\dfrac{7-4\sqrt{3}+\left|2-\sqrt{3}\right|}{3\left|2-\sqrt{3}\right|-1}=\dfrac{7-4\sqrt{3}+2-\sqrt{3}}{3\left(2-\sqrt{3}\right)-1}=\dfrac{9-5\sqrt{3}}{5-3\sqrt{3}}=\dfrac{\left(9-5\sqrt{3}\right)\left(5+3\sqrt{3}\right)}{\left(5-3\sqrt{3}\right)\left(5+3\sqrt{3}\right)}=\dfrac{45+2\sqrt{3}-45}{-2}=-\sqrt{3}\)
Thay \(x=7-4\sqrt{3}\) vào P, ta được:
\(P=\dfrac{7-4\sqrt{3}+2-\sqrt{3}}{6-3\sqrt{3}-1}\)
\(=\dfrac{9-5\sqrt{3}}{5-3\sqrt{3}}=-\sqrt{3}\)


\(a,19^2=\left(18+1\right)^2=18^2+2.18.1+1^2=324+36+1=361\)
\(28^2=\left(27+1\right)^2=27^2+2.27.1+1^2=729+54+1=784\)
\(81^2=\left(80+1\right)^2=80^2+2.80.1+1^2=6400+160+1=6561\)
\(91^2=\left(90+1\right)^2=90^2+2.90.1+1^2=8100+180+1=8281\)
\(b,19.21=\left(20-1\right)\left(20+1\right)=20^2-1^2=400-1=399\)
\(29.31=\left(30-1\right)\left(30+1\right)=30^2-1^2=900-1=899\)
\(39.41=\left(40-1\right)\left(40+1\right)=40^2-1^2=1600-1=1599\)
\(c,28^2-8^2=\left(28-8\right)\left(28+8\right)=20.36=720\)
\(56^2-46^2=\left(56-46\right)\left(56+46\right)=10.102=1020\)
\(67^2-57^2=\left(67-57\right)\left(67+57\right)=10.124=1240\)
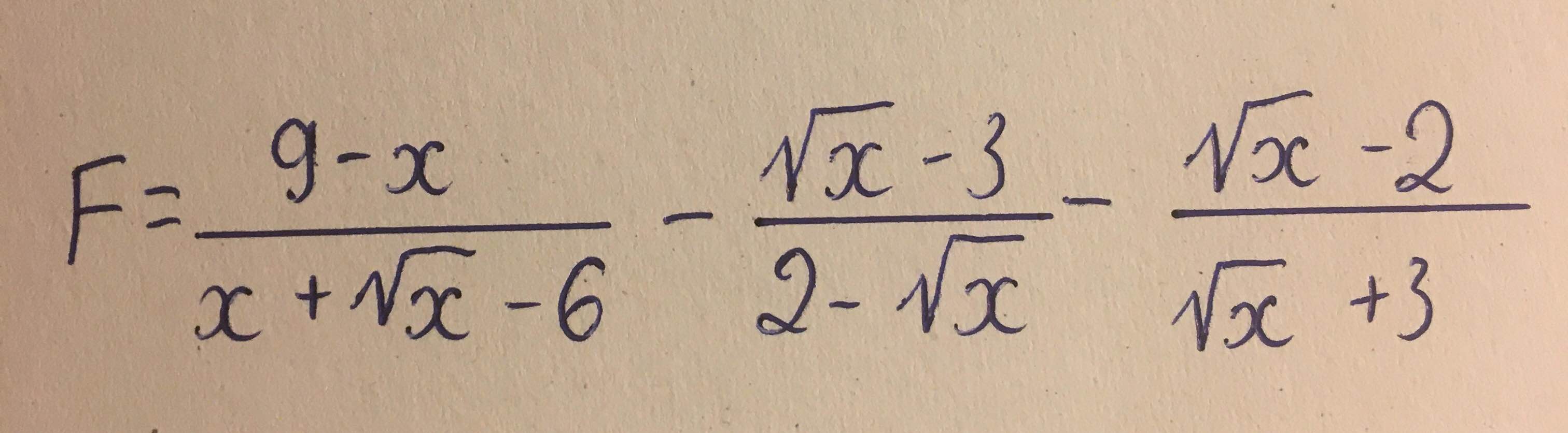



\(F=\dfrac{9-x}{x+\sqrt{x}-6}-\dfrac{\sqrt{x}-3}{2-\sqrt{x}}-\dfrac{\sqrt{x}-2}{\sqrt{x}+3}\left(đk:x\ne4\right)=\dfrac{9-x+\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}-2\right)}{x+\sqrt{x}-6}=\dfrac{9-x+x-9-\left(\sqrt{x}-2\right)^2}{x+\sqrt{x}-6}=\dfrac{-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\dfrac{2-\sqrt{x}}{\sqrt{x}+3}\)
\(F=\dfrac{9-x}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}+\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}-\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{9-x+x-9-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\) \(=\dfrac{-\left(\sqrt{x}-2\right)^2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\dfrac{1}{3-\sqrt{x}}\)