Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu \(x \in (0;5]\) thì thuế thu nhập cá nhân là: \(x.5\% = 0,05x\)
Nếu \(x \in (5;10]\) thì thuế thu nhập cá nhân là: \(x.10\% = 0,1x\)
Nếu \(x \in (10;18]\) thì thuế thu nhập cá nhân là: \(x.15\% = 0,15x\)
Nếu \(x \in (18;32]\) thì thuế thu nhập cá nhân là: \(x.20\% = 0,2x\)
Nếu \(x \in (32;52]\) thì thuế thu nhập cá nhân là: \(x.25\% = 0,25x\)
Nếu \(x \in (52;80]\) thì thuế thu nhập cá nhân là: \(x.30\% = 0,3x\)
Nếu \(x \in (80; + \infty )\) thì thuế thu nhập cá nhân là: \(x.35\% = 0,35x\)
Vậy công thức tính thuế thu nhập cá nhân là:
\(y = \left\{ \begin{array}{l}0,05x\quad \quad 0 < x \le 5\\0,1x\quad \;\;\quad 5 < x \le 10\\0,15x\quad \quad 10 < x \le 18\\0,2x\quad \;\;\;\;\;18 < x \le 32\\0,25x\quad \quad 32 < x \le 52\\0,3x\quad \quad \;\,52 < x \le 80\\0,35x\quad \quad 80 < x\end{array} \right.\)

a) Thu nhập trung bình của thành viên trong công ty là
\(\bar X = \frac{{20.1 + 4.5}}{6} = \frac{{40}}{6} \approx 6,67\)
Vậy thu nhập trung bình của các thành viên là 6,67 triệu đồng.
b) Ta thấy rõ ràng thu nhập của giám đốc cao hơn thu nhập trung bình rất nhiều (khoảng 13,3 triệu), còn thu nhập của mỗi nhân viên thì gần với thu nhập trung bình hơn (khoảng 2,67 triệu). Như thế, thu nhập trung bình không phản ánh đúng thu nhập của nhân viên công ty.
Chú ý
Công ty có 6 người thì cần tính thu nhập trung bình của 6 người.

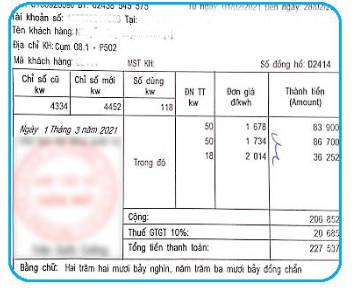
Quan sát hóa đơn ta thấy:
Tổng lượng điện tiêu thụ trong tháng là: 50 + 50 + 18 = 118 (kW).
Số tiền phải trả (chưa tính thuế giá trị gia tăng) là 206 852 đồng.
Giá tiền điện được tính theo bậc thang cho từng số lượng điện đã dùng, cụ thể:
Dùng 50 kW đầu thì đơn giá là 1 678 đồng/ 1 kW.
Dùng 50 kW tiếp theo thì đơn giá là 1 734 đồng/ 1 kW.
Dùng 100 kW tiếp thì đơn giá là 2 014 đồng/ 1 kW.
…
Ở hóa đơn điện trên kia, người sử dụng điện dùng 118 kW, có nghĩa phải trả theo 3 bậc.
Nên ta tính số tiền điện bằng cách thực hiện phép tính:
50 . 1 678 + 50 . 1 734 + 18 . 2 014 = 206 852 (đồng)
Vậy ta mô tả được sự phụ thuộc của số tiền điện phải trả vào tổng lượng điện tiêu thụ như trên.

Chọn B.
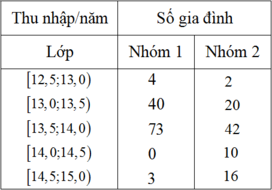
Ta tính mức thu nhập trung bình của mỗi nhóm
+ Số trung bình của thu nhập gia đình/năm của nhóm 1

+ Số trung bình thu nhập gia đình/năm của nhóm 2

Như vậy; mức thu nhập cùa nhóm 2 cao hơn.

Tham khảo:
a)
Bước 1: Ta có:
| Loại A | Loại B |
Giá mua vào | 10 triệu đồng/1 máy | 20 triệu đồng/1 máy |
Lợi nhuận | 2,5 triệu đồng/1 máy | 4 triệu đồng/1 máy |
Bước 2: Lập hệ bất phương trình
Vì số lượng máy là số tự nhiên nên ta có \(x \ge 0;y \ge 0\)
Vốn nhập vào x máy loại A và y máy loại B là \(10x + 20y\)(triệu đồng)
4 tỉ đồng=4000 (triệu đồng)
Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có bất phương trình
\(10x + 20y \le 4000\) \( \Leftrightarrow x + 2y \le 400\)
Vì tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy nên ta có \(x + y \le 250\).
Vậy ta có hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Bước 3: Xác định miền nghiệm
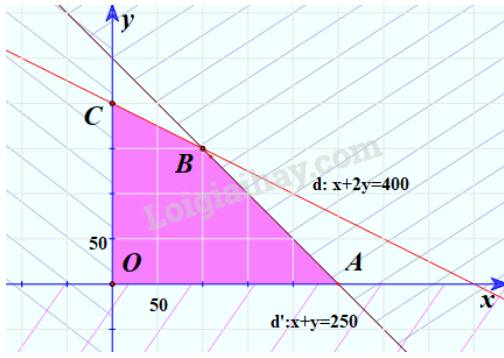
Miền nghiệm là tứ giác OABC với tọa độ các đỉnh này là O(0;0), A(250;0), B(100;150), C(0;200)
b) Lợi nhuận hàng tháng là F(x;y)=2,5x+4y(triệu đồng)
c) Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Ta có F(0;0)=0, F(250;0)=2,5.250+4.0=625
F(100;150)=2,5.100+4.150=850
F(0;200)=2,5.0+4.200=800
Giá trị lớn nhất là F(100;150)=850.
Vậy cửa hàng cần đầu tư kinh doanh 100 máy A và 150 máy B.
a) Số máy tính loại A cửa hàng cần nhập trong một tháng là x (máy), số máy tính loại B cửa hàng cần nhập trong một tháng là y (máy) (x,y≥0).
Do tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy: x + y ≤ 250
Tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)
Vì mỗi chiếc máy tính loại A có giá 10 triệu và mỗi máy tính loại B có giá 20 triệu nên tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)
Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có: 10x + 20y ≤ 4 000 hay x + 2y ≤ 400.
Ta có hệ bất phương trình: \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)
Ta xác định miền nghiệm của hệ bất phương trình trên:
+) Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0).
+) Miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0;1).
+) Xác định miền nghiệm D3 của bất phương trình x + y ≤ 250.
- Vẽ đường thẳng d: x + y = 250.
- Vì 0 + 0 = 0 < 250 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + y ≤ 250
Do đó miền nghiệm D3 của bất phương trình x + y ≤ 250 là nửa mặt phẳng bờ d chứa gốc tọa độ.
+) Xác định miền nghiệm D4 của bất phương trình x + 2y ≤ 400.
- Vẽ đường thẳng d’: x + 2y = 400.
- Vì 0 + 2.0 = 0 < 400 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + 2y < 400
Do đó miền nghiệm D4 của bất phương trình x + 2y < 400 là nửa mặt phẳng bờ d’ chứa gốc tọa độ.
Miền nghiệm của hệ bất phương trình trên là tứ giác OABC với O(0;0), A(0; 200), C(100;150), B(250;0)
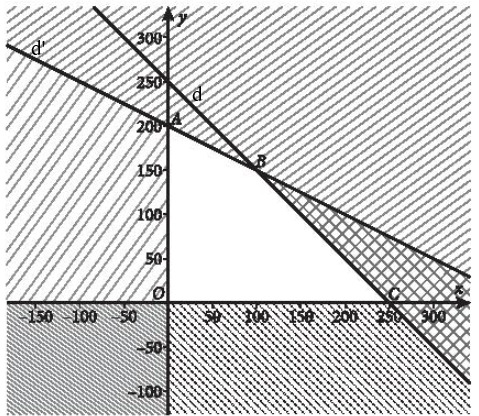
b) Lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B là: F(x;y) = 2,5x + 4y (triệu đồng).
Vậy F(x;y) = 2,5x + 4y.
c) Bài toán chuyển về tìm giá trị lớn nhất của F(x;y) với (x;y) thuộc miền nghiệm của hệ bất phương trình \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)
Người ta đã chứng minh được, giá trị F(x; y) lớn nhất tại (x; y) là tọa độ của một trong bốn đỉnh O; A; B; C.
Tại O(0; 0), ta có: F(0; 0) = 2,5 . 0 + 4 . 0 = 0;
Tại A(0; 200), ta có: F(0; 200) = 2,5 . 0 + 4 . 200 = 800;
Tại B(100; 150), ta có: F(100; 150) = 2,5 . 100 + 4 . 150 = 850;
Tại B(250; 0), ta có: F(250; 0) = 2,5 . 250 + 4 . 0 = 625.
Do đó F(x;y) lớn nhất bằng 850 tại x = 100 và y = 150.
Vậy cửa hàng cần nhập 100 máy loại A, 150 máy loại B để cửa hàng thu được lợi nhuận lớn nhất là 850 triệu đồng.

15 triệu đồng = 15000 nghìn đồng
Từ giả thiết bài toán ta có bất phương trình \(p\left( x \right) \ge 15000 \Leftrightarrow - 30{x^2} + 2100x - 15000 \ge 15000\)
\( \Rightarrow - 30{x^2} + 2100x - 30000 \ge 0\)
Xét tam thức \(f\left( x \right) = - 30{x^2} + 2100x - 30000\) có \(\Delta = 810000 > 0\), có hai nghiệm phân biệt là \({x_1} = 20,{x_2} = 50\) và \(a = - 30 < 0\)
Ta có bảng xét dấu như sau

Nếu muốn lợi nhuận không dưới 15 triệu đồng một tháng thì giá bán trung bình của các món ăn cần nằm trong khoảng 20 đến 50 nghìn đồng.

a) Nhà máy A:
+) Số trung bình: \(\overline x = \frac{{4 + 5 + 5 + 47 + 5 + 6 + 4 + 4}}{8} = 10\)
+) Mốt: \({M_o} = 4,{M_o} = 5\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 4; 4; 4; 5; 5; 5; 6; 47.
\({Q_2} = {M_e} = 5\)
\({Q_1}\) là trung vị của nửa số liệu: 4; 4; 4; 5. Do đó \({Q_1} = 4\)
\({Q_3}\) là trung vị của nửa số liệu: 5; 5; 6; 47. Do đó \({Q_3} = 5,5\)
+) Phương sai \({S^2} = \frac{1}{8}\left( {{4^2} + {5^2} + ... + {4^2}} \right) - {10^2} = 196\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} = 14\)
Nhà máy B:
+) Số trung bình: \(\overline x = \frac{{2 + 9 + 9 + 8 + 10 + 9 + 9 + 11 + 9}}{9} = 8,4\)
+) Mốt: \({M_o} = 9\)
+) Tứ phân vị: \({Q_1},{Q_2},{Q_3}\)
Sắp xếp mẫu số liệu theo thứ tự không giảm: 2; 8; 9; 9; 9; 9; 9; 10; 11
\({Q_2} = {M_e} = 9\)
\({Q_1}\) là trung vị của nửa số liệu: 2; 8; 9; 9. Do đó \({Q_1} = 8,5\)
\({Q_3}\) là trung vị của nửa số liệu: 9; 9; 10; 11. Do đó \({Q_3} = 9,5\)
+) Phương sai \({S^2} = \frac{1}{9}\left( {{2^2} + {9^2} + ... + {9^2}} \right) - 8,{4^2} = 6,55\) => Độ lệch chuẩn \(S = \sqrt {{S^2}} = 2,56\)
b)
Nhà máy A có: \({\Delta _Q} = 1,5\)
Vậy giá trị ngoại lệ \(x > 5,5 + 1,5.1,5 = 7,75\) hoặc \(x < 4 - 1,5.1,5 = 1,75\) là 47.
Nhà máy B có: \({\Delta _Q} = 1\)
Vậy giá trị ngoại lệ \(x > 9,5 + 1,5.1 = 11\) hoặc \(x < 8,5 - 1,5.1 = 7\) là 2.
Ta so sánh trung vị: \(9 > 5\), do dó công nhân nhà máy B có mức lương cao hơn.
Chú ý
Ta không so sánh số trung bình vì có giá trị 47 quá lớn so với các giá trị còn lại.


a)
Với mức thu nhập x (triệu đồng) không quá 5 triệu đồng thì thuế suất tương ứng là 5%.
Công thức hàm số bậc nhất mô tả sự phụ thuộc của thuế thu nhập cá nhân vào phần thu nhập tính thuế/tháng là: \(y = x.5\% = 0,05x\) với \(0 < x \le 5\).
Vẽ đổ thị hàm số:
Hàm số đi qua gốc tọa độ O (0;0) và điểm A (2;0,1)
b) Hāy lập công thức hàm số bậc nhất mô tả sự phụ thuộc của thuế thu nhập cá nhân vào phần thu nhập tinh thuế/tháng với mức thu nhập tính thuế/tháng trên 5 triệu đồng và không quá 10 triệu đồng. Vẽ đổ thị hàm số này.
Với mức thu nhập x (triệu đồng) trên 5 triệu đồng và không quá 10 triệu đồng thì thuế suất tương ứng là 10%.
Công thức hàm số bậc nhất mô tả sự phụ thuộc của thuế thu nhập cá nhân vào phần thu nhập tính thuế/tháng là: \(y = x.10\% = 0,1x\) với \(5 < x \le 10\)
Vẽ đổ thị hàm số:
Hàm số đi điểm B (6;0,6) và điểm C (10;1)
c)
Thu nhập tính thuế (số tiền sau khi đã tính các khoản giảm trừ) là:
\(28 - 11 - 4,4 = 12,6\) (triệu đồng)
Vì \(10 < 12,6 < 18\) nên thuế suất tương ứng là 15%.
Do đó số thuế thu nhập cá nhân mà anh Nam phải nộp trong 1 tháng là:
\(12,6.15\% = 1,89\) (triệu đồng)
Vậy số thuế thu nhập cá nhân mà anh Nam phải nộp trong 1 năm là:
\(1,89.12 = 22,68\) (triệu đồng)