Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quãng đường vật rơi nửa thời gian đầu:
![]()
Quãng đường vật rơi nửa thời gian cuối
![]()
Quãng đường vật rơi: h = h 1 + h 2
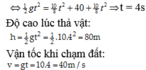

Đáp án D
Quãng đường vật rơi nửa thời gian đầu:
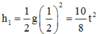
Quãng đường vật rơi nửa thời gian cuối
![]()
Quãng đường vật rơi:
![]()
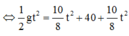
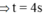
Độ cao lúc thả vật:
![]()
Vận tốc khi chạm đất:
v = gt = 10.4 = 40m/s

\(s_2-s_1=40\Leftrightarrow s-s_1-s_1=40\Leftrightarrow s-2s_1=40\)
\(\Rightarrow\dfrac{1}{2}gt^2-2\cdot\dfrac{1}{2}gt_1^2=40\)
Mà: \(t_1=\dfrac{1}{2}t\Rightarrow\dfrac{1}{2}gt^2-2\cdot\dfrac{1}{2}g\left(\dfrac{1}{2}t\right)^2=40\)
\(\Leftrightarrow\dfrac{1}{4}gt^2=40\Leftrightarrow t=\sqrt{\dfrac{40}{\dfrac{1}{4}g}}=\sqrt{\dfrac{40}{\dfrac{1}{4}\cdot10}}=4\left(s\right)\)
\(\Rightarrow\left\{{}\begin{matrix}h=s=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot10\cdot4^2=80\left(m\right)\\v=gt=10\cdot4=40\left(m/s\right)\end{matrix}\right.\)
Vậy: h = 80 (m), t = 4 (s) và v = 40 (m/s).

a, Ta có:v=g.t⇔80=10.t⇔t=8s
⇒s=\(\dfrac{1}{2}\)g.t2=320m
b,140=\(\dfrac{1}{2}\)g.t2⇔t2=28⇔t=2√7s

Ta có: \(h=\dfrac{1}{2}gt^2=5t^2\)
Thời gian để vật rơi ở quãng đường h - 10 là:
\(h-10=\dfrac{1}{2}gt'^2=5t^2-10=5t'^2\)
\(\Rightarrow t'^2=t^2-2\)
\(\Rightarrow t^2-t'^2=2\left(1\right)\)
Mà \(t-t'=0,2\left(2\right)\)
Từ (1) và (2) \(\Rightarrow t=5,1s\)
Tốc độ của vật khi chạm đất: \(v=v_0+gt=0+10+5,1=51\)m/s
Độ cao h: \(h=v_0t=\dfrac{1}{2}st^2=0.5,1+\dfrac{1}{2}10\left(5,1\right)^2=130,05m\)

a. áp dụng công thức \(v1^2-v0^2=2as\) \(\Rightarrow70^2=2.10.s\Leftrightarrow s=245\) m
b. áp dụng công thức v=gt \(\Rightarrow70=10.t\Leftrightarrow t=7\) s
a, Áp dụng ct liên hệ giữa gia tốc , vận tốc và quãng đường đi dc
\(v^2-v_0^2=2as\Rightarrow70^2-0^2=2\cdot10s\Rightarrow s=245\left(m\right)\)
Vậy ...
b, Thời gian rơi của vật:
\(s=\dfrac{1}{2}gt^2\Rightarrow t^2=\dfrac{s}{\dfrac{1}{2}g}=\dfrac{245}{\dfrac{1}{2}\cdot10}=49\Rightarrow t=7\left(s\right)\left(t>0\right)\)
