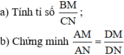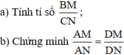Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Xét tứ giác AMDN có
góc AMD=góc AND=góc MAN=90 độ
AD là phan giác
=>AMDN là hình vuông
2: BC=căn 3^2+4^2=5cm
AD là phân giác
=>DB/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=5/7
=>BD=15/7cm; CD=20/7cm

a: ΔABC vuông tại A
=>AB^2+AC^2=BC^2
=>BC^2=15^2+20^2=625
=>BC=25cm
Xét ΔABC có AD là phân giác
nên \(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos45=\dfrac{2\cdot15\cdot20}{15+20}\cdot\dfrac{\sqrt{2}}{2}=\dfrac{60\sqrt{2}}{7}\)
b: ΔABC vuông tại A có AH là đường cao
nên AH*BC=AB*AC
=>AH*25=15*20=300
=>AH=12cm
ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC
=>BH=AB^2/BC=15^2/25=9cm
CH=25-9=16cm
c: góc AID=góc BIH=90 độ-góc DBC
góc ADI=90 độ-góc ABD
mà góc ABD=góc DBC
nên góc AID=góc ADI
=>ΔADI cân tại A

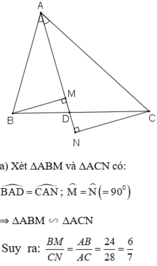
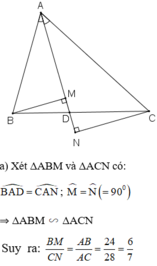
a) Tính BM/CN ?
*tgiác DMB đồng dạng tgiác DNC
=> BM/CN = DB/DC (1)
*Do tính chất của phân giác ta có:
DB/DC = AB/AC = 24/28 = 6/7 (2)
Từ (1) và (2): BM/CN = 6/7
b)cm AM/AN = DM/DN ?
*gt: góc BAD = góc DAC
=> tgiác AMB đồng dạng tgiác ANC
=> AM/AN = AB/AC (3)
*mà ta biết tgiác DMB đồng dạng tgiác DNC
=> DM/DN = DB/DC
do(2) => DM/DN = AB/AC (4)
*Từ (3) và (4) => AM/AN = DM/DN

Vì AD là ph/giac tgiac ABC\(\Rightarrow\frac{AB}{AC}=\frac{BD}{DC}\left(1\right)\)
Có \(\frac{S_{ABD}}{S_{ADC}}=\frac{\frac{1}{2}.BD.AH}{\frac{1}{2}.DC.AH}=\frac{BD}{DC}\left(2\right)\)
(1) và (2) suy ra ĐPCM

Kẻ đường cao AH
Ta có:AD là phân giác góc BAC nên \(\frac{BD}{DC}=\frac{AB}{AC}\) (1)
Ta có:\(\frac{S_{ABD}}{S_{ACD}}=\frac{\frac{1}{2}AH\cdot BD}{\frac{1}{2}AH\cdot CD}=\frac{BD}{CD}\) (2)
Từ (1) và (2)\(\Rightarrow\frac{S_{ABD}}{S_{ACD}}=\frac{AB}{AC}=\frac{4}{6}=\frac{2}{3}\)