Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Gọi A a ; a 3 − 3 a 2 thuộc đồ thị hàm số y = x 3 − 3 x 2
PTTT tại A là: y = 3 a 2 − 6 a x − a + a 3 − 3 a 2
Tiếp tuyến đi qua M nên
m = 3 a 2 − 6 a 2 − a + a 3 − 3 a 2 = − 2 a 3 + 9 a 2 − 12 a *
Để kẻ được 3 tiếp tuyến thì PT (*) có 3 nghiệm phân biệt
Xét hàm số
f a = − 2 a 3 + 9 a 2 − 12 a ⇒ f ' a = − 6 a 2 + 18 a − 12 = 0 ⇔ a = 2 a = 1
Khi đó (*) có 3 nghiệm phân biệt khi và chỉ khi m ∈ f 1 ; f 2 = − 5 ; − 4 .

Đường thẳng qua A m ; - m có dạng y = k(x-m) - m
Hệ điều kiện tiếp xúc: 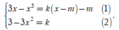
Thay (2) vào (1) ta được:
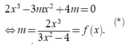
Yêu cầu bài toán ⇔ phương trình (*) có nghiệm duy nhất.
Lập bảng biến thiên và kết luận m ∈ - 2 ; 2 . Suy ra P = 8. Chọn D.

Đáp án B
Phương trình đường thẳng có hệ số góc k, đi qua M(m;2) là y - 1 = k(x - m) (d)
Vì (d) tiếp xúc với (C) khi và chỉ khi k = f ' x k x - m + 2 = - x 3 + 6 x 2 + 2 ⇔ k = - 3 x 2 + 12 x k x - m = - x 3 + 6 x 2
⇔ - 3 x 2 + 12 x x - m + x 3 - 6 x 2 = 0 ⇔ [ x = 0 - 3 x + 12 x x - m + x 2 - 6 x = 0
⇔ [ x = 0 - 3 x 2 + 3 m x + 12 x - 12 m + x 2 - 6 x = 0 ⇔ [ x = 0 2 x 2 - 3 m + 2 x + 12 m = 0 *
Để từ M kẻ được 2 tiếp tuyến tới đồ thị (C) khi và chỉ khi:
TH1. Phương trình (*) có nghiệm kép khác 0 ⇔ ∆ = 9 m + 2 2 - 96 m = 0 ⇔ [ m = 6 m = 2 3
TH2. Phương trình (*) có nghiệm kép bằng 0, nghiệm còn lại khác 0 ⇔ 12 m = 0 ∆ > 0 ⇔ m = 0
Vậy m = 0 ; 2 3 ; 6 là các giá trị cần tìm → ∑ m = 0 + 2 3 + 6 = 20 3 .

Chọn đáp án C
Tập xác định: D = R.
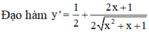
Gọi ∆ là đường thẳng đi qua M 0 ; m và có hệ số góc là k, phương trình đường thẳng ∆ : y = k x + m .
Đường thẳng ∆ là tiếp tuyến của (C) khi và chỉ khi hệ phương trình sau có nghiệm :
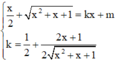
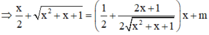
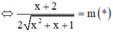
Hệ phương trình trên có nghiệm khi và chỉ khi phương trình (*) có nghiệm
Xét hàm số f x = x + 2 2 x 2 + x + 1 trên R.
Đạo hàm
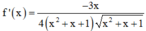
![]()
Bảng biến thiên
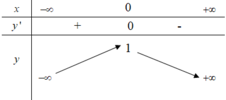
Dựa vào bảng biến thiên ta thấy: Phương trình (*) có nghiệm
⇔ - 1 2 < m ≤ - 1 hay m ∈ ( - 1 2 ; 1 ] .
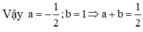
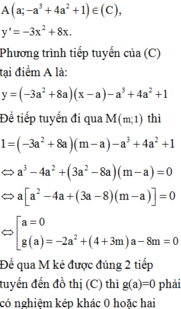
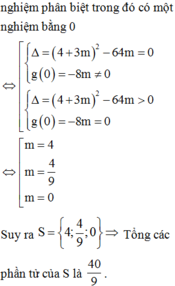
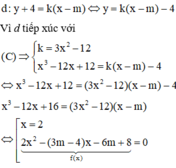
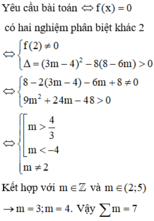



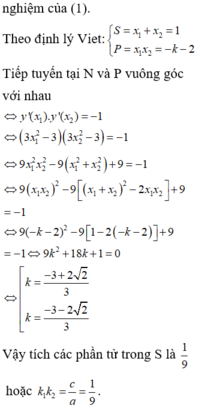
Chọn A