Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có 
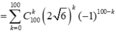
Phần thực của z tương ứng với k là bội của 2, vậy phần thực bằng
là một số nguyên dương.
Chọn đáp án A.
Đáp án A
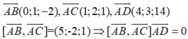
⇒ A B → , A C → , A D → đồng phẳng suy ra tồn tại vô số mặt phẳng cách đều 4 điểm trên
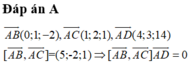
⇒ A B → , A C → , A D → đồng phẳng suy ra tồn tại vô số mặt phẳng cách đều 4 điểm trên
Đáp án B
Ta có
A
B
→
=
-
1
;
2
;
0
A
D
→
=
1
;
-
2
;
0
⇒
A
B
→
+
A
D
→
=
0
⇒
A
,
B
,
D
thẳng hàng
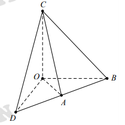
Do đó, 5 điểm O, A, B, C, D tạo thành tứ diện như hình vẽ bên
Vậy có tất cả 5 mặt phẳng cần tìm đó là:
+ Mặt phẳng (OAC) đi qua 3 điểm O, A, C.
+ Bốn mặt phẳng là các mặt bên của tứ diện O.BCD đi qua 3 điểm trong 5 điểm O, A, B, C, D.
Đáp án B
A B → - 1 ; 2 ; 0 , A D → 1 ; - 2 ; 0 , A B → = - A D → ⇒ A , B , D thẳng hàng
Cứ 3 điểm không thẳng hàng cho ta một mặt phẳng
Số cách chọn 3 trong 5 điểm trên là C 5 3 = 10
A,B,D thẳng hàng nên qua 3 điểm này không xác định được mặt phẳng
Số cách chọn 2 trong và điểm A,B,D và 1 điểm trong O và C là: C 3 2 . C 2 1 = 6
Nếu chọn 2 trong 3 điểm A,B,D kết hợp cùng hai điểm còn lại sẽ ra một số mặt phẳng trùng nhau. Nên trường hợp này ta chỉ xác định được 2 mặt phẳng phân biệt
Vậy số mặt phẳng phân biệt đi qua 3 điểm O,A,B,C,D là: 10-1-6+2=5
Đáp án A
Phương trình mặt phẳng (ABC) là x 1 + y 3 + z 2 = 1 mà D 1 ; 3 ; - 2 ⇒ D ∈ A B C .
Và ta thấy rằng A C ¯ = - 1 ; 0 ; 2 và B D ¯ = - 1 ; 0 ; 2 suy ra ABCD là hình bình hành.
Vậy O.ABCD là một hình chóp có đáy là hình bình hành, do đó có 5 mặt phẳng thỏa mãn yêu cầu gồm:
Mặt phẳng đi qua trung điểm của AC,BD và song song với (SAD) hoặc (SBC).
Mặt phẳng đi qua trung điểm cuả AD,BC đồng thời song song với (SAC) hoặc (SBD).
Mặt phẳng đi qua trungđiểm của OA,OB,OC,OD.
Đáp án B
Mặt phẳng cách đều 5 điểm là mặt phẳng mà khoảng cách từ 5 điểm đó đến mặt phẳng là bằng nhau.
Có 5 mặt phẳng thỏa mãn là:
+ Mặt phẳng đi qua trung điểm của AB,CD và song song với SBC .
+ Mặt phẳng đi qua trung điểm của AB,CD và song song với SAD .
+ Mặt phẳng đi qua trung điểm của AD,BC và song song với SAB .
+ Mặt phẳng đi qua trung điểm của AD,BC và song song với SCD .
+ Mặt phẳng đi qua trung điểm của SA,SB,SC,SD.
Đáp án đúng : D