Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
BA,BE là tiếp tuyến
=>BA=BE
mà OA=OE
nên OB là trung trực của AE
=>OB vuông góc AE
=>BH*BO=BA^2
ΔABC vuông tại A có AD vuông góc BC
nên BD*BC=BA^2
=>BH*BO=BD*BC
b: BH*BO=BD/BC
=>BH/BC=BD/BO
=>góc BHD=góc BCO
=>góc DHO+góc DCO=180 độ
=>DHOC nội tiếp

Em tham khảo tại link dưới đây nhé.
Câu hỏi của My Trấn - Toán lớp 9 - Học toán với OnlineMath
Với câu c, khi đã có IK // AD thì vận dụng Ta let ta có ngay \(\frac{IC}{AD}=\frac{IK}{AD}\Rightarrow IC=IK\)

a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xét (O) có
DC là tiếp tuyến
DA là tiếp tuyến
Do đó: DC=DA
Xét (O) có
EC là tiếp tuyến
EB là tiếp tuyến
Do đó: EC=EB
Ta có: DC+CE=DE
nên DE=DA+EB
b: Xét tứ giác ADCO có \(\widehat{DAO}+\widehat{DCO}=180^0\)
nên ADCO là tứ giác nội tiếp
=>\(\widehat{ADO}=\widehat{ACO}\)
mà \(\widehat{ACO}=\widehat{CAB}\)
nên \(\widehat{ADO}=\widehat{CAB}\)

Em tham khảo tại link dưới đây nhé.
Câu hỏi của My Trấn - Toán lớp 9 - Học toán với OnlineMath
Với câu c, khi đã có IK // AD thì vận dụng Ta let ta có ngay \(\frac{IC}{AD}=\frac{IK}{AD}\Rightarrow IC=IK\)
Với câu c
Kẻ BC cắt DA tại một điểm là P
Ta có : DO//CD(...)
AO=OB(...)
==> DP=DA
Ta lại có: DA//EB. ==> IA/IE=AD/BE
Mà AD=CD; BE=CE(Tính chất 2 tt cắt nhau)
==>IA/IE=CD/CE ==> CI//AD. ==> CK//DA
. CI//PD. ==> CI/PD=BI/BD
. IK//DA ==> IK/DA=BI/BD
==> CI/PD=IK/DA
Mà PD=DA(..) ==>CI=IK

a) Chứng minh AE.AC=AH.AD:
Xét \(\Delta\)AEH và \(\Delta\)ADC: ^AEH=^ADC(=900); ^DAC chung => \(\Delta\)AEH ~ \(\Delta\)ADC (g.g)
\(\Rightarrow\frac{AE}{AD}=\frac{AH}{AC}\Rightarrow AE.AC=AH.AD\)(đpcm).
b) Chứng minh P;H;Q thẳng hàng:
Ta nối 2 điểm P và Q với điểm H.
Xét đường tròn (I): Có AQ là tiếp tuyến; AEC là cát tuyến => ^AQE=^ACQ
Xét \(\Delta\)AEQ và \(\Delta\)AQC: ^QAC chung; ^AQE=^ACQ => \(\Delta\)AEQ ~ \(\Delta\)AQC (g.g)
\(\Rightarrow\frac{AQ}{AC}=\frac{AE}{AQ}\Rightarrow AQ^2=AE.AC\)
Lại có: \(AE.AC=AH.AD\Rightarrow AQ^2=AH.AD\Rightarrow\frac{AQ}{AH}=\frac{AD}{AQ}\)
Xét \(\Delta\)AHQ và \(\Delta\)AQD: ^DAQ chung; \(\frac{AQ}{AH}=\frac{AD}{AQ}\)=> \(\Delta\)AHQ ~ \(\Delta\)AQD (c.g.c)
\(\Rightarrow\)^AQH=^ADQ (1)
Ta thấy: AP và AQ là 2 tiếp tuyến của (I) => Tứ giác APIQ nội tiếp đường tròn (Tâm là trung điểm AI)
Dễ có tứ giác ADIQ nội tiếp đường tròn tâm là trung điểm AI (Do ^ADI=^AQI=900)
Từ đó suy ra: 5 điểm A;P;D;I;Q cùng thuộc 1 đường tròn => Tứ giác APDQ nội tiếp dường tròn
=> ^ADQ=^APQ (Cùng chắn cung AQ) (2)
Từ (1) và (2) => ^AQH=^APQ. Mà \(\Delta\)PAQ cân đỉnh A => ^APQ=^AQP => ^AQH=^AQP
Dễ thấy 2 tia QH và QP nằm cùng phía so với mặt phẳng bờ là AQ
=> P;H;Q là 2 điểm thẳng hàng (đpcm).
c) Chứng minh HP vuông với AK và KH vuông với AI:
Ở phần c) Mình sửa điểm P thành điểm R vì phần b) đã có điểm P rồi.
+) Ta có: Tứ giác BFEC nội tiếp (I) => ^ECB=^BFK hay ^KCE=^KFB
=> \(\Delta\)KBF ~ \(\Delta\)KEC (g.g) => \(\frac{KB}{KE}=\frac{KF}{KC}\Rightarrow KB.KC=KE.KF\)(3)
Xét đường tròn (O) có 2 cát tuyến KRA và KBC, ta có ngay tỉ số: \(\frac{KR}{KC}=\frac{KB}{KA}\Rightarrow KB.KC=KR.KA\)(4)
Từ (3) và (4) => \(KE.KF=KR.KA\)\(\Rightarrow\frac{KR}{KE}=\frac{KF}{KA}\)
=> \(\Delta\)KRF ~ \(\Delta\)KEA (c.g.c) => ^KRF=^KEA. Mà ^KRF+^FRA=1800
=> ^KEA+^FRA=1800 hay ^FRA+^FEA=1800 => Tứ giác ARFE nội tiếp đường tròn.
Mà tứ giác AFHE nội tiếp đường tròn => 5 điểm A;R;F;H;E cùng thuộc 1 đường tròn
=> Tứ giác ARFH nội tiếp đường tròn => ^ARH=^AFH.
Lại có: ^AFH=900 => ^ARH=900 => HR vuông góc AR hay HR vuông góc AK (ddpcm0.
+) Gọi giao điểm của tia RH và (O) là M => ^ARM=^ARH=900
Tứ giác ARBM nội tiếp đường trong nên ^ARM=^ABM (=900) => AB vuông góc BM
Lại thấy CF vuông góc AB => CF//BM hay CH//BM
Tứ giác ABMC nội tiếp đường tròn => ^ABM+^ACM=1800 => ^ACM=900
Tương tự ta c/m được: CM//BH
Xét tứ giác BHCM: CH//BM; CM//BH (cmt) => Tứ giác BHCM là hình bình hành
Do I là trung điểm BC nên H.I.M thẳng hàng => R;H;I thẳng hàng và IR vuông góc AK
Xét \(\Delta\)KAI: IR vuông AK; AD vuông KI; IR cắt AD tại H => H là trực tâm của \(\Delta\)KAI
=> KH vuông góc với AI (đpcm).
d) Chứng minh BC;EF;PQ đồng quy:
Vì EF cắt BC tại điểm K nên ta sẽ chứng minh K;P;Q là 3 điểm thẳng hàng.
Dễ có: Tứ giác APDI nội tiếp đường tròn => ^DPI=^DAI.
Mà ^DAI=^IKH (Cùng phụ góc AIK) => ^DPI=^IKH hay ^DPI=^DKP
Xét \(\Delta\)KPD: ^DKP + ^KDP+^KPD = 1800 => ^DPI + ^KDP + ^KPD = 1800
=> ^KPI + ^KDP = 1800 (5)
Để ý rằng tứ giác PDIQ nội tiếp đường tròn => ^IQP=^KDP.
Mà \(\Delta\)PIQ cân đỉnh I => ^IQP=^IPQ => ^KDP=^IPQ (6)
Từ (5) và (6) => ^KPI + ^IPQ = 1800 => ^KPQ = 1800 => 3 điểm K;P;Q thẳng hàng.
Qua đó, ta suy ra được BC;EF;PQ đồng quy (đpcm).

Em tham khảo tại link dưới đây nhé.
Câu hỏi của My Trấn - Toán lớp 9 - Học toán với OnlineMath
Với câu c, khi đã có IK // AD thì vận dụng Ta let ta có ngay \(\frac{IC}{AD}=\frac{IK}{AD}\Rightarrow IC=IK\)

a) a1. Chứng minh \(BAOE\) là tứ giác nội tiếp.
Tứ giác \(BAOE:\left\{{}\begin{matrix}\hat{OEB}=90^o\left(\text{tiếp tuyến}\right)\\\hat{OAB}=90^o\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\hat{OEB}+\hat{OAB}=90^o+90^o=180^o\Rightarrow BAOE\) là tứ giác nội tiếp (đpcm).
a2. Chứng minh : \(BH.BO=BD.BC\).
Ta có : \(\hat{ADC}=90^o\) (góc nội tiếp chắn nửa đường tròn)
\(\Rightarrow AD\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BD.BC=AB^2\left(1\right).\)
Mặt khác : \(\left\{{}\begin{matrix}OA=OE=R\left(gt\right)\\AB=BE\left(\text{tính chất hai tiếp tuyến cắt nhau}\right)\end{matrix}\right.\)
\(\Rightarrow OB\) là đường trung trực của \(AE\Rightarrow\hat{AHB}=90^o\)
\(\Rightarrow AH\) là đường cao của \(\Delta ABC\) vuông tại \(A\Rightarrow BH.BO=AB^2\left(2\right).\)
Từ \(\left(1\right),\left(2\right)\Rightarrow BH.BO=BD.BC\) (đpcm).
b) b1. Chứng minh \(DHOC\) là tứ giác nội tiếp.
Tứ giác \(AHDB:\hat{AHB}=\hat{ADB}=90^o\left(cmt\right)\). Mà hai góc này có đỉnh kề nhau trong tứ giác và cùng nhìn cạnh \(AB\) nên đây là tứ giác nội tiếp \(\Rightarrow\hat{ABH}=\hat{ADH}.\)
Mà : \(\left\{{}\begin{matrix}\hat{ADH}+\hat{HDC}=90^o\left(=\hat{ADC}\left(cmt\right)\right)\\\hat{ABH}+\hat{HAB}=90^o\left(\text{hai góc phụ nhau}\right)\end{matrix}\right.\Rightarrow\hat{HDC}=\hat{HAB}\left(3\right).\)
Mặt khác : \(\hat{AOB}=\hat{HAB}\left(\text{cùng phụ }\hat{ABH}\right)\left(4\right).\)
Từ \(\left(3\right),\left(4\right)\Rightarrow\hat{AOB}=\hat{HDC}\Rightarrow DHOC\) là tứ giác nội tiếp (dấu hiệu nhận biết) (đpcm).
b2. Chứng minh : \(\hat{BHD}=\hat{OHC}\).
Do \(DHOC\) là tứ giác nội tiếp (cmt) \(\Rightarrow\hat{OCD}=\hat{BHD}\left(5\right)\) (cùng bù với \(\hat{OHD}\)) và \(\hat{OHC}=\hat{ODC}\left(6\right)\) (hai góc có đỉnh kề nhau cùng nhìn cạnh \(OC\)).
Mặt khác : \(OA=OD=R\Rightarrow\Delta OAD\) cân tại \(O\Rightarrow\hat{ODA}=\hat{OAD}.\)
Và : \(\left\{{}\begin{matrix}\hat{OAD}+\hat{OCD}=90^o\left(\text{hai góc phụ nhau}\right)\\\hat{ODA}+\hat{ODC}=90^o\left(=\hat{ADC}\right)\end{matrix}\right.\Rightarrow\hat{OCD}=\hat{ODC}\left(7\right).\)
Từ \(\left(5\right),\left(6\right),\left(7\right)\Rightarrow\hat{BHD}=\hat{OHC}\) (đpcm).
c) Chưa nghĩ ra ạ:)
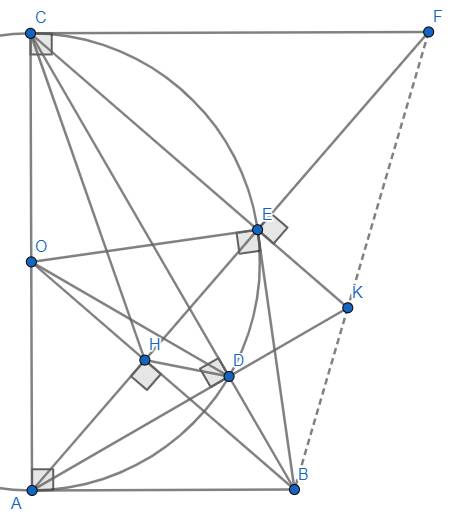
Gọi I là giao của AE và CD
AE vuông góc KC
CD vuông góc AK
=>I là trực tâm của ΔACK
=>KI vuông góc AC
=>KI//AB
góc BHD=góc OHC
=>90 độ-góc BHD=90 độ-góc OHC
góc DHI=góc CHI
=>HI là phân giác của góc CHD
HB vuông góc HI
=>HB là phân giác góc ngoài của ΔCHD
BD/BC=HD/HC
=>ID/IC=BD/BC
=>BC/IC=BD/ID
KI//AB//CD
=>AB/KI=AB/ID=BC/IC=AF/IF
ΔKIF đồng dạng vói ΔBAF
=>góc KFI=góc BFA
=>B,K,F thẳng hàng