Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- vẽ MH và MK lần lượt vuông góc với AB và AC
- Xét \(\Delta AHM\)vuông tại H và\(\Delta AKM\)vuông tại K có: AM: cạnh chung
\(\widehat{HAM}=\widehat{KAM}\)(vì AM là tia phân giác của \(\widehat{A}\))
\(\Rightarrow\)\(\Delta AHM=\Delta AKM\)(cạnh huyền - góc nhọn)
\(\Rightarrow\)MH = MK (2 cạnh tương ứng)
- Xét \(\Delta BHM\)vuông tại H và\(\Delta CKM\)vuông tại K có: BM = CM ( M là trung diểm của BC)
HM = KM (cmt)
\(\Rightarrow\)\(\Delta BHM=\Delta CKM\)(cạnh huyền - cạnh góc vuông)
\(\Rightarrow\)\(\widehat{B}=\widehat{C}\)(2 góc tương ứng)
Vậy \(\Delta ABC\)cân tại A ( vì có góc B và góc C là 2 góc ở đáy bằng nhau )

thì vừa là đường trung tuyến vừa là đường trung trực thì tam giác đó cân chứ sao trời!

a: Xét ΔCAM vuông tại A và ΔCNM vuông tại N có
CM chung
góc ACM=góc NCM
=>ΔCAM=ΔCNM
b: Xét ΔMAK vuông tại A và ΔMNB vuông tại N có
MA=MN
góc AMK=góc NMB
=>ΔMAK=ΔMNB
=>MK=MB

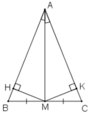
Kẻ MH ⊥ AB, MK ⊥ AC
Xét hai tam giác vuông AHM và AKM, ta có:
∠(AHM) =∠(AKM) = 90o
Cạnh huyền AM chung
∠(HAM) = ∠KAM) (gt)
⇒ ΔAHM = ΔAKM (cạnh huyền, góc nhọn)
Suy ra: MH = MK (hai cạnh tương ứng)
Xét hai tam giác vuông MHB và MKC, ta có:
∠(MHB) = ∠(MKC) = 90o
MB = MC ( vì M là trung điểm BC).
MH = MK (chứng minh trên)
⇒ ΔMHB = ΔMKC (cạnh huyền, cạnh góc vuông)
Suy ra: ∠B = ∠C (hai góc tương ứng)
Vậy tam giác ABC cân tại A.

a: Xét ΔADM và ΔAEM có
AD=AE
AM chung
DM=EM
Do đó: ΔADM=ΔAEM
Suy ra: \(\widehat{DAM}=\widehat{EAM}\)
hay AM là tia phân giác của \(\widehat{BAC}\)

-Cách 2: -Kẻ MH vuông góc với AB; MK vuông góc với AC( H thuộc AB và K thuộc AC).
-Ta có: tam giác AHM= tam giác AKM( cạnh huyền-góc nhọn).
=> HM=MK. => tam giác BHM= tam giác CKM( cạnh huyền-cạnh góc vuông).
=> góc HBM= góc KCM. => tam giác ABC cân tại A.(đpcm)

Xét tam giác ABM VÀ ACM:
Góc MAB= MAC ( do AM là tia phân giác)
AM: cạnh chung'
BM=BC ( do M là trung điểm BC)
=> tam giác ABM= ACM ( c.g.c)
vậy: AB=AC ( hai cạnh tương ứng)
suy ra: Tam giác ABC là tam giác cân
Ta có: M là trung điểm BC (gt) => AM là đường trung tuyến
Xét tam giác ABC có AM là đường trung tuyến đồng thời là đường phân giác
=> Tam giác ABC cân tại A (vì trong 1 tam giác, 1 đường mang 2 tên thì là tam giác cân)