Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
Ta có :
\(\widehat{DAC}=\widehat{EAB}\left(=90^0+\widehat{BAC}\right)\)
=> \(\Delta DAC=\Delta EAB\left(c.g.c\right)\)
=> DC = EB ( hai cạnh tương ứng )
b)
Gọi giao điểm của DC với BE ; BA lần lượt là H và I
Vì \(\Delta DAC=\Delta EAB\)(c/m câu a)
=> \(\widehat{DAI}=\widehat{IBH}\)
Mà \(\widehat{DIA}=\widehat{HIB}\)( đối đnhr )
=> \(\widehat{DAI}=\widehat{IHB}=90^0\)
a) Xét \(\Delta ADC,\Delta ABE\) có:
AD = AB ( gt )
\(\widehat{DAC}=\widehat{EAB}\left(=90^o+\widehat{BAC}\right)\)
AE = AC ( gt )
\(\Rightarrow\Delta DAC=\Delta EAB\left(c-g-c\right)\)
\(\Rightarrow DC=BE\) ( 2 cạnh tương ứng ) ( đpcm )
b) Gọi giao điểm giữa DC và AB là K
giao điểm giữa DC và BE là M
Ta có: \(\widehat{ADK}+\widehat{K_1}=90^o\) ( do \(\Delta DAK\) có \(\widehat{DAK}=90^o\) ) (1)
Vì \(\Delta ADC=ABE\)
\(\Rightarrow\widehat{ADC}=\widehat{ABE}\) ( 2 góc tương ứng )
hay \(\widehat{ADK}=\widehat{KBE}\) (2)
Mà \(\widehat{K_1}=\widehat{K_2}\) ( đối đỉnh ) (3)
Xét (1), (2) và (3) ta có:
\(\widehat{ADK}+\widehat{K_1}=90^o\)
Mà \(\widehat{ADK}=\widehat{KBE}\)
\(\widehat{K_1}=\widehat{K_2}\)
\(\Rightarrow\widehat{KBE}+\widehat{K_2}=90^o\)
Xét \(\Delta KBM\) có \(\widehat{KBE}+\widehat{K_2}=90^o\Rightarrow\widehat{KMB}=90^o\)
\(\Rightarrow BE\perp DC\left(đpcm\right)\)

a) Xét tam giác ADC và AEB ta có :
AB =AC (gt)
góc CAD = BAE (2 góc tương ứng)
AD =AE
Suy ra tam giác ADC = AEB
Suy ra DC = BE

a) xét tg AMC và tg ABN có
MA=BA(gt)
CA=AN(gt)
ˆMAC=ˆBAN(doˆMAB+ˆBAC=ˆNAC+ˆBAC)MAC^=BAN^(doMAB^+BAC^=NAC^+BAC^)
=>(kết luận)...
b)gọi I là giao điểm của MC và BN
gọi giao điểm của BA và MI là F
vì ΔAMC=ΔABNΔAMC=ΔABNnên
ˆFMA=ˆFBIFMA^=FBI^
mà ˆFMA+ˆFMB=45OFMA^+FMB^=45O
=>ˆFBI+ˆIMB=45OFBI^+IMB^=45O
Xét ΔIMBΔIMBcó góc ˆIMB+ˆMBI+ˆBIMIMB^+MBI^+BIM^= 180O
Mà ˆIMB+ˆMBIIMB^+MBI^=900
=>...

a) Ta có: góc DAC= góc DAB + góc BAC
góc BAE= góc EAC+ góc CAB
Mà góc DAB= góc EAC=90 độ
=> góc DAC= góc BAE
Xét tam giác DAC và tam giác BAE có:
AD=AB
góc DAC= góc BAE
AC=AE
=> tam giác DAC= tam giác BAE ( c.g.c)
=> DC=BE
Gọi I và H lần lượt là giao điểm của DC với AB và BE
Ta có: góc D+ góc DAH+ góc DHA= góc B+ góc BHI+ góc BIH= 180 độ
Mà góc D= góc B ( tam giác DAC= tam giác BAE) va góc DHA = góc BHI ( hai góc đôi đỉnh)
=> góc DAH= góc BIH
Mà góc DAH=90 độ=> góc BIH=90 độ=> DC vuông góc vs BE

\(\sqrt{\sqrt[]{}\frac{ }{ }\hept{\begin{cases}\\\end{cases}}\hept{\begin{cases}\\\\\end{cases}}^{ }\orbr{\begin{cases}\\\end{cases}}_{ }_{ }^2\widehat{ }\widebat{ }\overline{ }\overrightarrow{ }^{ }_{ }\underrightarrow{ }|^{ }_{ }\cot\sin\cos\tan\sinh\cosh\tanh\Leftrightarrow}\)

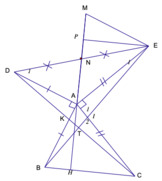

Xét tam giác ADC và tam giác ABE có
AD = AB ( gt )
Góc DAB = Góc CAE = 90 độ và cùng cộng với góc BAC
AC = AE ( gt )
Tam giác ADC bằng Tam giác ABE ( c.g.c )
DC = BE ( hai cạnh tương ứng )
Góc ADC = góc ACE ( hai góc tương ứng )
Gọi giao điểm của AB và DC là O, giao điểm dC và BE là I
Ta có góc ADO bằng góc ABI ( cmt ), góc ADO bằng góc ABD ( tam giác ADB vuông cân )
Xét tam giác ABO và tam giác OBI có
Góc DOA = góc BOI ( đối đỉnh )
AB = AD
Góc ADO = góc ABI
2 tam giác bằng nhAu
Góc DAO = Góc DIO ( hai giác tương ứng ) và bằng 90 độ
Be vuông góc với DC