NH
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NH
0
PT
1
CM
15 tháng 4 2017
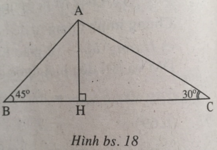
Vẽ đường cao AH. Đặt BH = x, CH = y thì do H nằm giữa B và C (hai góc ∠ B, ∠ C là góc nhọn) suy ra x + y = 4 (xem h.bs.18).
Ta có BH = AH = HC.tg 30 ° nên x – y.tg 30 ° = y/ 3
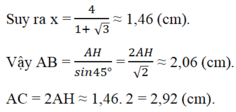
AC = 2AH ≈ 1,46. 2 = 2,92 (cm).
CC
1
29 tháng 8 2015
Tam giác ABC vuông tại A, B=60.
\(\Rightarrow\) Tam giác ABC là 1 nửa tam giác đều
\(\Rightarrow AB=\frac{BC}{2}\) =4; AC=12-4=8
DT
1
30 tháng 7 2020
Vẽ đường cao AH . Đặt BH = x, CH = y thì do H nằm giữa B và C ( hai góc \(\widehat{B } ; \widehat{C}\) là góc nhọn) suy ra x + y = 4
Ta có \(BH=AH=HC.tg30^o\)nên \(x-y.tg30^o=y\sqrt{3}\)
\(\Rightarrow x=\frac{4}{1+\sqrt{3}}\approx1,46\left(cm\right)\)
Vậy \(AB=\frac{AH}{\sin45^o}=\frac{2AH}{\sqrt{2}}\approx2,06\left(cm\right)\)
\(AC=2AH\approx1,46.2=2,92\left(cm\right)\)
AC = 2AH ≈ 1,46. 2 = 2,92 ( cm )