Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Phương pháp: Δ φ = 2 π d λ
Cách giải:
+ Áp dụng hệ thức lượng trong tam giác vuông OMN có đường cao OH:
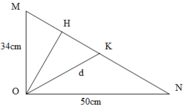
1 O H 2 = 1 O M 2 + 1 O N 2 ⇔ 1 O H 2 = 1 34 2 + 1 50 2 ⇒ O H = 28,1 c m
+ Gọi d là khoảng cách từ O đến K (K là 1 điểm bất kì trên MN)
+ Độ lệch pha giữa K và O là: Δ φ = 2 π d λ
+ Để K dao động cùng pha với O thì: Δ φ = 2 π d λ = 2 k π ⇒ d = k λ
+ Số điểm dao động cùng pha với o trên đoạn MN bằng số giá trị k nguyên thoả mãn:
28,1 ≤ k λ ≤ 34 ⇒ 7,025 ≤ k ≤ 8,5 ⇒ k = 8 28,1 < k λ ≤ 50 ⇒ 7,025 < k ≤ 12,5 ⇒ k = 8 ; 9 ; 10 ; 11 ; 12
Có 6 giá trị của k thoả mãn ⇒ trên đoạn MN có 6 điểm dao động cùng pha với nguồn

Đáp án C

+ Bước sóng: λ = v/f = 0,6/40 = 1,5cm
+ Số cực đại giao thoa trên đoạn thẳng nối hai nguồn bằng số giá trị k nguyên thoả mãn:

+ Áp dụng định lí Pi – ta – go trong tam giác vuông AMB có:
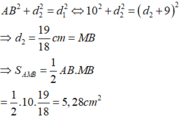

Đáp án B
Phương pháp: Sử dụng lí thuyết về giao thoa sóng hai nguồn cùng pha và áp dụng công thức tính số cực đại trên đoạn thẳng nối hai nguồn
Cách giải:
Hình ảnh giao thoa:
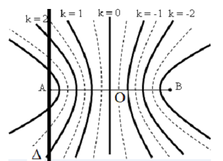
+ Số cực đại trên đoạn AB bằng số giá trị k nguyên thoả mãn:
− A B λ < k < A B λ ⇔ − 16 3 < k < 16 3 ⇔ − 5,3 < k < 5,3 ⇒ k = 0 ; ± 1 ; ... ; ± 5
+ Trong khoảng từ A đến O có 5 đường hypebol cực đại. Mỗi đường cắt ( ∆ ) tại 2 điểm ⇒ Trên ( ∆ ) có 10 điểm dao động với biên độ cực đại
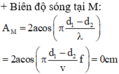
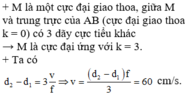




Đáp án D