Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
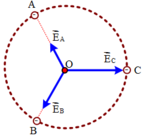
![]()
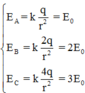
Từ
![]()
vì không có tính đối xứng nên ta có thể tổng hợp theo phương pháp số phức (chọn véc tơ E C → làm chuẩn)
![]()
![]()
![]()
![]()

a.Vì q1 > 0 mà chúng đẩy nhau nên q2 > 0
F= \(\frac{k.\left|q_1q_2\right|}{r^2}\)
\(\Rightarrow\left|q_2\right|=\frac{F.r^2}{\left|q_1\right|}=\frac{6,75.10^{-5}.0,02^2}{\left|4.10^{-8}\right|}=0,675\left(C\right)\)
=>q2 =0,675 C
b)
b) \(E_{q_1}=\frac{k.\left|q_1\right|}{BH^2}=\frac{9.10^9.\left|4.10^{-8}\right|}{0,01^2}=3,6.10^6\frac{V}{m}\)
\(E_{q_2}=\frac{k.\left|q_2\right|}{AH^2}=\frac{9.10^9.\left|0,675\right|}{0,01^2}=6,075.10^{13}\frac{V}{m}\)
Vì vecto E1 ↑↑ vecto E2=>E=|E1-E2|=6,075.1013 V/m
\(E_{q_3}=\frac{k.\left|q_3\right|}{AH^2}=\frac{9.10^9.\left|-2.10^{-8}\right|}{\left(0,02.\sin45^o\right)^2}=621,5.10^3\frac{V}{m}\)
Vì vecto E vuông góc với Eq3 nên:
EH =\(\sqrt{E_{q_3}^2+E^2}=6,075.10^{13}\left(\frac{V}{m}\right)\)

a, 
khoảng từ tâm D đến các cạnh \(r=\dfrac{2}{3}.\sqrt{6^2-3^2}=2\sqrt{3}\)
ta có\(F_1=F_2=F_3=k\dfrac{\left|q_1.q_0\right|}{\left(2\sqrt{3}.10^{-2}\right)^2}=7,5\left(N\right)\)
ta tổng lực F2 và F3 với cosa=120 độ
\(F_{23}=\sqrt{F_2^2+F_3^2+2F_2F_3cos\alpha}=7,5\left(N\right)\)
theo phương chiều như hình vẽ ta có \(F=\left|F_{23}-F_1\right|=0\)
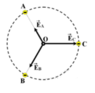


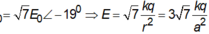
E → O = E → A + E → B + E → C = E → A + E → B C → E → A ↑ ↑ E → B C E O = E A + E B C
Trong đó: E A = E B C = k q O A 2 → O A = 2 3 a 2 − a 2 2 = 9.10 3 V m
→ E → A ↑ ↑ E → B C E O = E A + E B C = 18.10 3