Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Vẽ vecto \(\overrightarrow {AB} \) là vecto vận tốc của máy bay, \(\overrightarrow {AD} \) là vecto vận tốc của gió.
Khi đó vecto vận tốc mới của máy bay là \(\overrightarrow {AB} + \overrightarrow {AD} \)
Dựng hình bình hành ABCD. Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\)
Mà AB = 700, BC = AD = 40, \(\widehat B = {135^o}\)
\(\begin{array}{l} \Rightarrow A{C^2} = {700^2} + {40^2} - 2.700.40.\cos {135^o} \approx 531197,98\\ \Leftrightarrow AC \approx 728,83\end{array}\)
Vậy tốc độ mới của máy bay là 728,83 km/h.

Chọn C.
Áp dụng công thức đổi rad sang độ ![]()
Ta được số đo góc cần tính là: ![]()

Gọi: vận tốc thực tế của tàu là \(\overrightarrow v \)
Vận tốc riêng của tàu (đối với dòng nước) là \(\overrightarrow {{v_t}} \)
Vận tốc của dòng nước (đối với bờ) là \(\overrightarrow {{v_n}} \)
Ta có: \(\overrightarrow v = \overrightarrow {{v_n}} + \overrightarrow {{v_t}} \)
Để tàu sang bờ bên kia nhanh nhất thì vận tốc thực tế của tàu có hướng vuông góc với bờ.
Theo quy tắc hình bình hành thì \(\overrightarrow v \) là vecto đường chéo xuất phát từ gốc chung của vecto vận tốc riêng của tàu và vecto vận tốc dòng nước tác động lên tàu.

Tính trực tiếp.
Chú ý rằng 37 ο 15 ' phải đổi ra thập phân.
15 ’ = 1 / 4 . 1 o = 0 , 25 o ⇒ 37 o 15 ’ = 37 , 25 o .
Vì 1 o ≈ 0,0175 nên ta có 37,25 x 0,0175 ≈ 0,652.



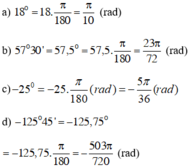
a) Đổi 35o47’25’’ sang radian
b) Đổi 3 rad ra độ